Redis算法
数据分布算法
普通Hash算法(modula)
比如你有 N 个 redis实例,那么如何将一个key映射到redis上呢,你很可能会采用类似下面的通用方法计算 key的 hash 值,然后均匀的映射到到 N 个 redis上:
hash(key)%N
如果增加一个redis,映射公式变成了 hash(key)%(N+1)
如果一个redis宕机了,映射公式变成了 hash(key)%(N-1)
在这两种情况下,每一个redis管理的数据全部要重新计算移动,几乎所有的缓存都失效了。会导致数据库访问的压力陡增,严重情况,还可能导致数据库宕机。
随机分配算法(random)
随机将数据分发到Redis集群中,Client无法准确地从某台机器获取相对的数据,该做法常用于消息队列中。
一致性Hash算法(ketama)
- 将内存想象成一个环,由于hash值有32位,因此将内存分出2 ^32(0~2 ^32-1)个地址
- 将节点的IP+算法确定唯一的哈希值,之后在内存中确定节点的位置
- 当保存数据时,根据key进行哈希运算,确定唯一的一个位置
- 根据当前
key位置顺时针查找最近的node节点进行挂载(在内存中,加法计算快于减法运算,因此采用顺时针查找)
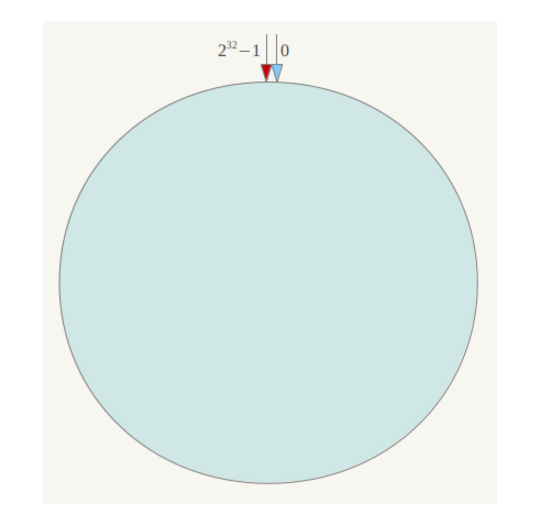
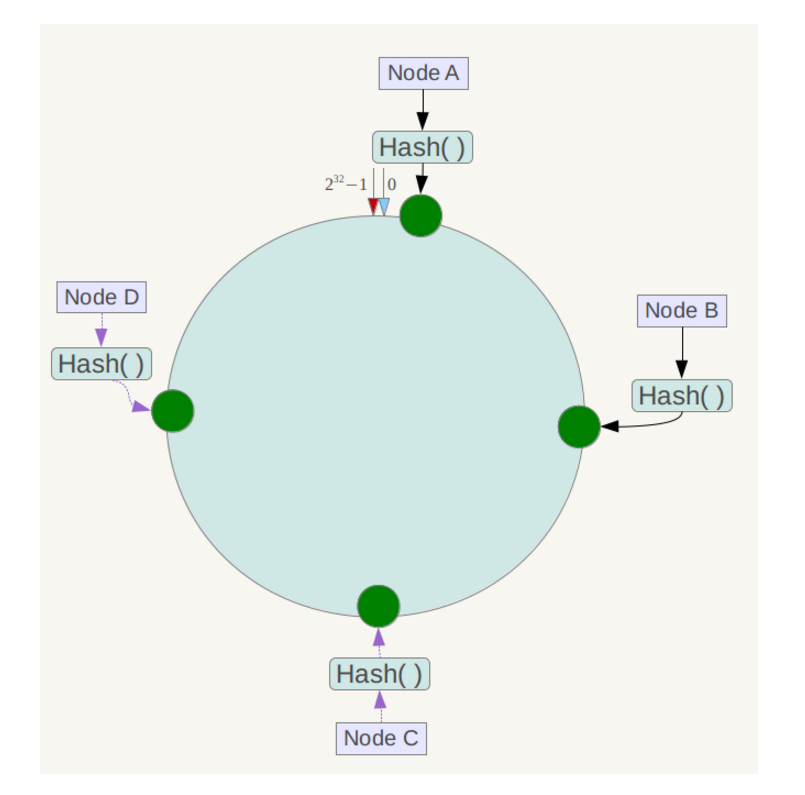
将各个服务器使用Hash进行一个哈希,具体可以选择服务器的ip或主机名作为关键字进行哈希,这样每台机器就能确定其在哈希环上的位置。
假设将中四台服务器使用ip地址哈希后在环空间的位置如下:
将数据key使用相同的函数Hash计算出哈希值,并确定此数据在环上的位置,从此位置沿环顺时针“行走”,第一台遇到的服务器就是其应该定位到的服务器。
假设4个存储对象 Object A、B、C、D,经过对 Key 的哈希计算后,它们的位置如下:
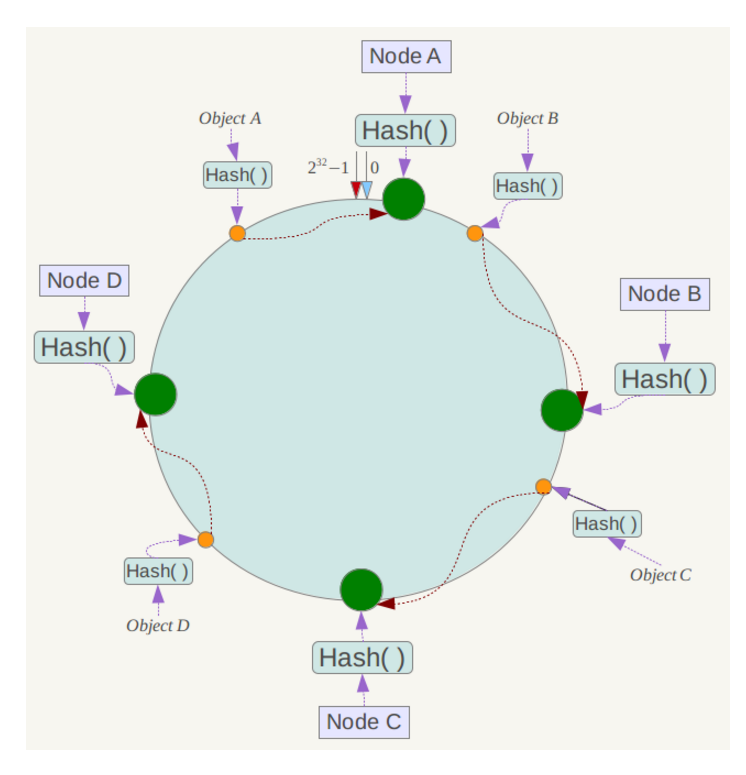
根据一致性哈希算法,数据A会被定为到Node A上,B被定为到Node B上,C被定为到Node C上,D被定为到Node D上。
容错性和可扩展性
假设Node C不幸宕机,可以看到此时对象A、B、D不会受到影响,只有C对象被重定位到Node D。一般的,在一致性哈希算法中,如果一台服务器不可用,则受影响的数据仅仅是此服务器到其环空间中前一台服务器(即沿着逆时针方向行走遇到的第一台服务器)之间数据,其它不会受到影响。
如果在系统中增加一台服务器Node X,如下图所示:
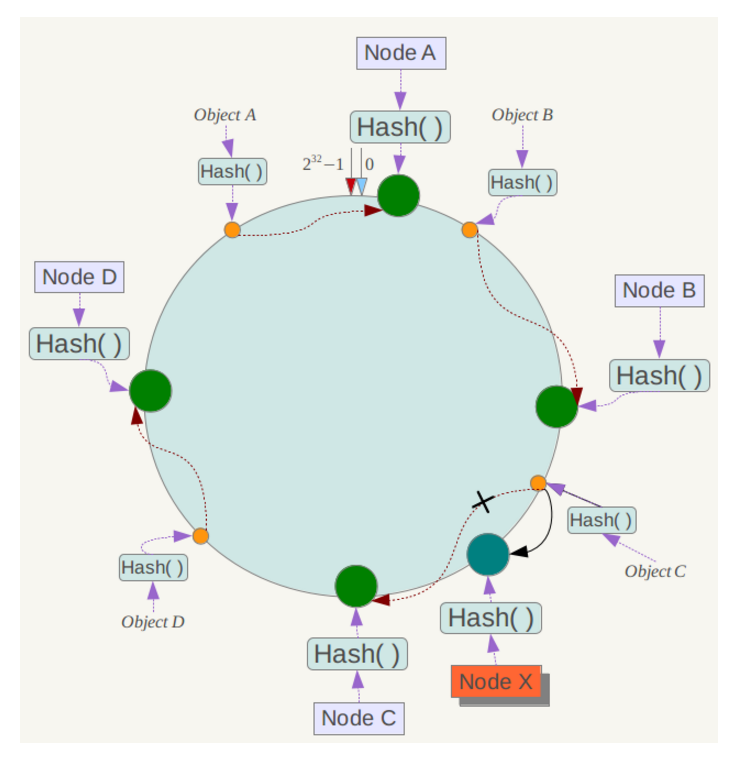
此时对象Object A、B、D不受影响,只有对象C需要重定位到新的Node X 。一般的,在一致性哈希算法中,如果增加一台服务器,则受影响的数据仅仅是新服务器到其环空间中前一台服务器(即沿着逆时针方向行走遇到的第一台服务器)之间数据,其它数据也不会受到影响。
综上所述,一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据,具有较好的容错性和可扩展性。
如果这时候新增了一个结点,对原来缓存的一部分数据的访问将会落到新增的结点上,但是这时候结点并没有数据缓存,它将去数据库中查找并缓存,原先已经缓存数据的结点需要通过淘汰算法(LRU)淘汰数据,它并没有从原缓存结点复制数据到新节点中。
虚拟节点
但一致性哈希算法也有一个严重的问题,就是数据倾斜。如果在分片的集群中,节点太少,并且分布不均,一致性哈希算法就会出现部分节点数据太多,部分节点数据太少。也就是说无法控制节点存储数据的分配。如下图,大部分数据都在 A 上了,B 的数据比较少。
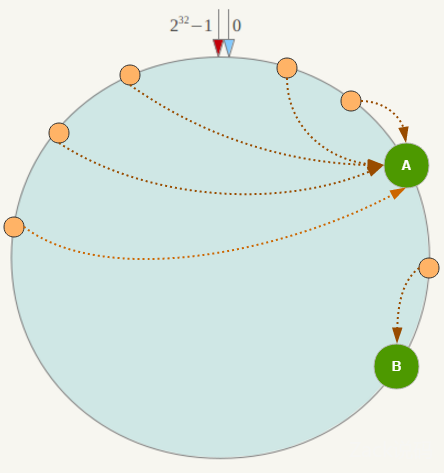
节点数越少,越容易出现节点在哈希环上的分布不均匀,导致各节点映射的对象数量严重不均衡(数据倾斜);相反,节点数越多越密集,数据在哈希环上的分布就越均匀。
以删除节点为例,假设删除了Node B节点,原来Node B节点的数据将转移到Node C上,这样Node C的内存使用率会骤增,如果Node B上存在热点数据,Node C会扛不住甚至会可能挂掉,挂掉之后数据又转移给Node D,如此循环会造成所有节点崩溃,也就是缓存雪崩。
为了解决雪崩现象和数据倾斜现象,提出了虚拟节点这个概念。就是将真实节点计算多个哈希形成多个虚拟节点并放置到哈希环上,定位算法不变,只是多了一步虚拟节点到真实节点映射的过程
但实际部署的物理节点有限,我们可以用有限的物理节点,虚拟出足够多的虚拟节点(Virtual Node),最终达到数据在哈希环上均匀分布的效果。
如下图,实际只部署了2个节点 Node A/B,每个节点都复制成3倍,结果看上去是部署了6个节点。可以想象,当复制倍数为 2^32 时,就达到绝对的均匀,通常可取复制倍数为32或更高。
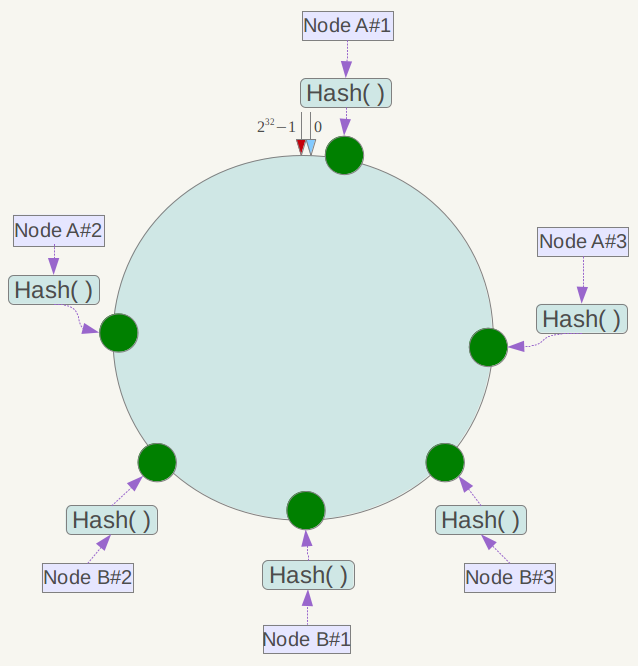
这就解决了雪崩的问题,当某个节点宕机后,其数据并没有全部分配给某一个节点,而是被分到了多个节点,数据倾斜的问题也随之解决。
实现
一致性哈希算法,既可以在客户端实现,也可以在中间件上实现(如 proxy)。在客户端实现中,当客户端初始化的时候,需要初始化一张预备的 Redis 节点的映射表:hash(key)=> . 这有一个缺点,假设有多个客户端,当映射表发生变化的时候,多个客户端需要同时拉取新的映射表。
另一个种是中间件(proxy)的实现方法,即在客户端和 Redis 节点之间加多一个代理,代理经过哈希计算后将对应某个 key 的请求分发到对应的节点,一致性哈希算法就在中间件里面实现。可以发现,twemproxy 就是这么做的。
哈希槽
redis 集群(cluster)并没有选用上面一致性哈希,而是采用了哈希槽(slot)的这种概念。主要的原因就是上面所说的,一致性哈希算法对于数据分布、节点位置的控制并不是很友好。
首先哈希槽其实是两个概念,第一个是哈希算法。redis cluster 的 hash 算法不是简单的hash(),而是 crc16 算法,一种校验算法。另外一个就是槽位的概念,空间分配的规则。
其实哈希槽的本质和一致性哈希算法非常相似,不同点就是对于哈希空间的定义。一致性哈希的空间是一个圆环,节点分布是基于圆环的,无法很好的控制数据分布。而 redis cluster 的槽位空间是自定义分配的,类似于 windows 盘分区的概念。这种分区是可以自定义大小,自定义位置的。
redis cluster 包含了16384个哈希槽,每个 key 通过计算后都会落在具体一个槽位上,而这个槽位是属于哪个存储节点的,则由用户自己定义分配。例如机器硬盘小的,可以分配少一点槽位,硬盘大的可以分配多一点。如果节点硬盘都差不多则可以平均分配。所以哈希槽这种概念很好地解决了一致性哈希的弊端。
当有新节点加入时,它不再需要像一致性Hash算法那样把每个key取出来重新计算hash值,只需要从旧节点中将新节点应该缓存的槽位数据拷贝到新节点中即可。
另外在容错性和扩展性上,表象与一致性哈希一样,都是对受影响的数据进行转移。而哈希槽本质上是对槽位的转移,把故障节点负责的槽位转移到其他正常的节点上。扩展节点也是一样,把其他节点上的槽位转移到新的节点上。
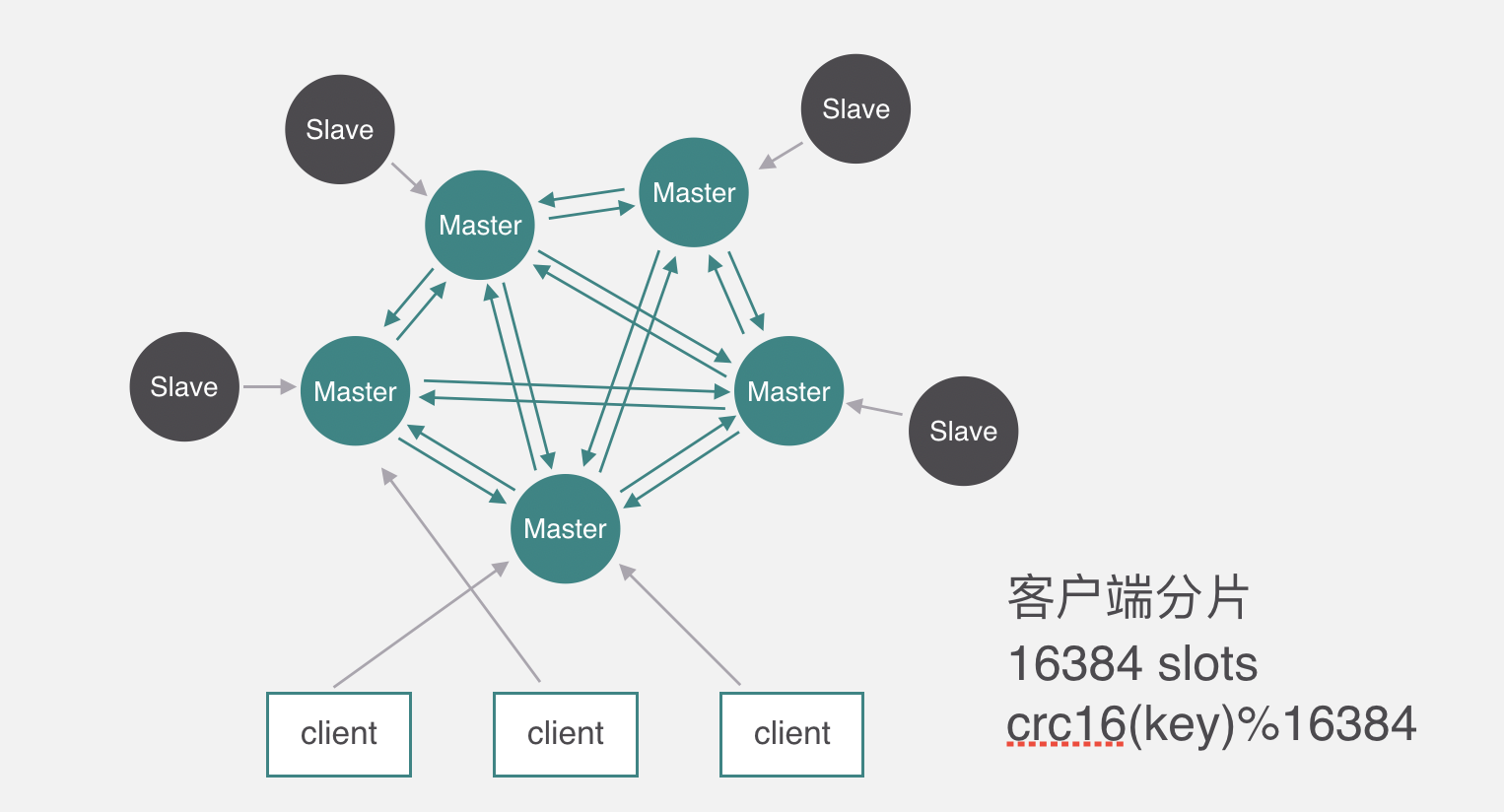
弊端是聚合操作很难实现,并且不支持跨机器事务,但是提供了Hash Tag让用户控制需要计算的Key都集中在一个Redis中。
缓存
缓存穿透
key对应的数据在数据源并不存在,每次针对此key的请求从缓存获取不到,请求都会到数据源,从而可能压垮数据源。比如用一个不存在的用户id获取用户信息,不论缓存还是数据库都没有,若黑客利用此漏洞进行攻击可能压垮数据库。
解决办法:
一个一定不存在缓存及查询不到的数据,由于缓存是不命中时被动写的,并且出于容错考虑,如果从存储层查不到数据则不写入缓存,这将导致这个不存在的数据每次请求都要到存储层去查询,失去了缓存的意义。
最常见的则是采用布隆过滤器,将所有可能存在的数据哈希到一个足够大的bitmap中,一个一定不存在的数据会被 这个bitmap拦截掉,从而避免了对底层存储系统的查询压力。
另外也有一个更为简单的方法,如果一个查询返回的数据为空(不管是数据不存在,还是系统故障),我们仍然把这个空结果进行缓存,但它的过期时间会很短,最长不超过五分钟。
缓存击穿
key对应的数据存在,但在redis中过期,此时若有大量并发请求过来,这些请求发现缓存过期一般都会从后端DB加载数据并回设到缓存,这个时候大并发的请求可能会瞬间把后端DB压垮。
业界比较常用的做法是使用互斥锁(mutex key),简单地来说,就是在缓存失效的时候(判断拿出来的值为空),不是立即去load db,而是先使用缓存工具的某些带成功操作返回值的操作,比如Redis的SETNX(SET if Not eXists),去set一个mutex key,当操作返回成功时,再进行load db的操作并回设缓存;否则,就重试整个get缓存的方法。
缓存雪崩
当缓存服务器重启或者大量缓存集中在某一个时间段失效,这样在失效的时候,也会给后端系统(比如DB)带来很大压力。
大多数系统设计者考虑用加锁或者队列的方式保证来保证不会有大量的线程对数据库一次性进行读写,从而避免失效时大量的并发请求落到底层存储系统上。
锁排队的解决方式分布式环境的并发问题,有可能还要解决分布式锁的问题;线程还会被阻塞,用户体验很差!因此,在真正的高并发场景下很少使用!
还有一个简单方案就是将缓存失效时间分散开,比如我们可以在原有的失效时间基础上增加一个随机值,比如1-5分钟随机,这样每一个缓存的过期时间的重复率就会降低,就很难引发集体失效的事件。
部分内容出自文章:
https://blog.csdn.net/qq_42695926/java/article/details/83090131
https://www.cnblogs.com/lihonglin2016/p/10039670.html
https://blog.csdn.net/kefengwang/java/article/details/81628977
最后更新: 2020年12月08日 09:17

