训练营三期

滑动窗口

1
2
3
给定一个有序数组arr，从左到右依次表示X轴上从左往右点的位置
给定一个正整数K，返回如果有一根长度为K的绳子，最多能盖住几个点
绳子的边缘点碰到X轴上的点，也算盖住
1
2
3
4
5
6
7
8
9
解法一：
假设以i为结尾，K的绳子盖住的点范围是：[i-k,i]，查询落在这个范围上的点有多少个
等同于查询[0..i-1]的范围上，有多少个数大于i-k，使用二分查找
每个下标都需要查找一次>i-k的位置,时间复杂度O(logN)，有N个点，则总体的时间O(N * logN)

解法二：
采用滑动窗口，LR一开始处于-1位置，R向右滑，滑到arr[R + 1] - arr[L] > K时停止，该答案是index = L答案
然后L++,再次判断 arr[R + 1] - arr[L] ?< K,若小于，则R++窗口继续滑动，周而复始
时间复杂度O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//二分方法
public static int maxPoint1(int[] arr, int L) {
    int res = 1;
    for (int i = 0; i < arr.length; i++) {
        int nearest = nearestIndex(arr, i, arr[i] - L);
        res = Math.max(res, i - nearest + 1);
    }
    return res;
}

public static int nearestIndex(int[] arr, int R, int value) {
    int L = 0;
    int index = R;
    while (L <= R) {
        int mid = L + ((R - L) >> 1);
        if (arr[mid] >= value) {
            index = mid;
            R = mid - 1;
        } else {
            L = mid + 1;
        }
    }
    return index;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//窗口滑动
public static int maxPoint2(int[] arr, int L) {
    int left = 0;
    int right = 0;
    int N = arr.length;
    int max = 0;
    while (left < N) {
        while (right < N && arr[right] - arr[left] <= L) {
            right++;
        }
        max = Math.max(max, right - (left++));
    }
    return max;
}

括号四连

1
2
3
4
5
6
7
括号有效配对是指：
1）任何一个左括号都能找到和其正确配对的右括号
2）任何一个右括号都能找到和其正确配对的左括号
有效的：    (())  ()()   (()())  等
无效的：     (()   )(     等
问题一：怎么判断一个括号字符串有效？
问题二：如果一个括号字符串无效，返回至少填几个字符能让其整体有效
1
2
3
4
5
6
7
问题一解法一：
把'('压栈，遇到')'则弹出，当还有')'且栈为空，或者遍历结束时栈不为空，返回false，其余返回true
问题一解法二：
使用一个Count计数，遇到'('则++，遇到')'则--，当count < 0 或者遍历结束后count != 0 ,返回false

问题二思路：
基于问题一解法二的基础知识下，再开一个need计数，当count < 0,则need++,遍历结束后,结果：need + count
1
2
3
4
5
6
7
8
9
10
11
12
//解法二
public static boolean valid(String s) {
    char[] str = s.toCharArray();
    int count = 0;
    for (int i = 0; i < str.length; i++) {
        count += str[i] == '(' ? 1 : -1;
        if (count < 0) {
            return false;
        }
    }
    return count == 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//问题二解法：
public static int needParentheses(String s) {
    char[] str = s.toCharArray();
    int count = 0;
    int need = 0;
    for (int i = 0; i < str.length; i++) {
        if (str[i] == '(') {
            count++;
        } else { // 遇到的是')'
            if (count == 0) {
                need++;
            } else {
                count--;
            }
        }
    }
    return count + need;
}
1
2
3
4
括号有效配对是指：
1）任何一个左括号都能找到和其正确配对的右括号
2）任何一个右括号都能找到和其正确配对的左括号
返回一个括号字符串中，最长的括号有效子串的长度
1
2
3
4
5
6
7
8
9
10
11
12
思路：
遇到这种子串的题目，优先思考以[i]开头，答案是什么...或者以[i]结尾，答案是什么...
如：   ( ) ( ) ( ( ) ) ( )
index:0 1 2 3 4 5 6 7 8 9

如果 arr[i] = '(' 以左括号结尾，无效，res[i] = 0,
如果 arr[i] = ')'获取res[i - 1] = k,判断 arr[i - k - 1] ?= '('，若不是，则res[i]=0
若是，则res[i]=k + 2 , 则至少确定了以arr[i - k - 1, i]是一个正确配对的答案
若再往前推，arr[i - k - 2] != 0,表示它前面还有能够拼接的正确括号,res[i] += arr[i - k - 2]

总结：
第i个位置，看i-1的答案和符号，匹配成功后，再往前跳一步看看是否还有正确的答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static int maxLength(String s) {
    if (s == null || s.length() < 2) {
        return 0;
    }
    char[] str = s.toCharArray();
    int[] dp = new int[str.length];
    int pre = 0;
    int ans = 0;
    // dp[0] = 0;
    for (int i = 1; i < str.length; i++) {
        if (str[i] == ')') {
            pre = i - dp[i - 1] - 1; // 与str[i]配对的左括号的位置 pre
            if (pre >= 0 && str[pre] == '(') {
                dp[i] = dp[i - 1] + 2 + (pre > 0 ? dp[pre - 1] : 0);
            }
        }
        ans = Math.max(ans, dp[i]);
    }
    return ans;
}
1
2
3
4
给一个正确的括号字符：((()))()(())() ,判断该字符中括号最大嵌套了几层？

思路：
弄个count计数，遇到'('，count++，遇到')'，count--，嵌套的层数就是count的最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static int deep(String s) {
    char[] str = s.toCharArray();
    if (!isValid(str)) {
        return 0;
    }
    int count = 0;
    int max = 0;
    for (int i = 0; i < str.length; i++) {
        if (str[i] == '(') {
            max = Math.max(max, ++count);
        } else {
            count--;
        }
    }
    return max;
}

辅助数组

1
2
3
4
有一些排成一行的正方形。每个正方形已经被染成红色或者绿色。
现在可以选择任意一个正方形然后用这两种颜色的任意一种进行染色,这个正方形的颜色将 会被覆盖。
目标是在完成染色之后,每个红色R都比每个绿色G距离最左侧近。 返回最少需要涂染几个正方形。
如样例所示: s = RGRGR 我们涂染之后变成RRRGG满足要求了,涂染的个数为2,没有比这个更好的涂染方案。
1
2
3
4
5
6
7
8
9
思想：
以每个index为分界线，左边涂R，右边涂G，分成两个数组，问题转换成左边数组中G出现的次数，右边R出现的次数
可以增加辅助数组X加速：缓存[i,N-1]上，R出现的次数
而辅助数组Y:[0,N-1]上，G出现的次数，这个信息可以从左往右遍历的时候通过一个信息left记录G出现的次数

进阶：
辅助数组X也可以省略掉，先获取数组中R出现的总次数rAll
在从左往右遍历的过程中，i遇到字符'R'，则rAll--，这时候rAll = [i + 1, N - 1]区间上R出现的次数
最后每个分界线的答案 = rAll + left
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// RGRGR -> RRRGG
public static int minPaint(String s) {
    if (s == null || s.length() < 2) {
        return 0;
    }
    char[] str = s.toCharArray();
    int N = str.length;
    //数组中R出现的总次数rAll
    int rAll = 0;
    for (int i = 0; i < N; i++) {
        rAll += str[i] == 'R' ? 1 : 0;
    }
    //单独先把R的数量赋值给ans，
    //因为边界线可能出现在 index = 0的左边，或者N-1 的右边，也就是全G或者全R的情况
    int ans = rAll; // 如果数组所有的范围，都是右侧范围，都变成G
    //[0,i]上，G出现的次数
    int left = 0;
    for (int i = 0; i < N - 1; i++) { // 0..i 左侧 n-1..N-1
        left += str[i] == 'G' ? 1 : 0;
        rAll -= str[i] == 'R' ? 1 : 0;
        ans = Math.min(ans, left + rAll);
    }
    // 0...N-1 左全部 右无
    ans = Math.min(ans, left + (str[N - 1] == 'G' ? 1 : 0));
    return ans;
}
1
2
3
4
5
6
7
8
给定一个N*N的矩阵matrix，只有0和1两种值，返回边框全是1的最大正方形的边长长度。
例如:
01111
01001
01001
01111
01011 
其中边框全是1的最大正方形的大小为4*4，所以返回4。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
思想：
总流程的时间复杂度一定是O(N^3),因为你任意一个正方形的左上角点，就是O(N^2)，然后还要根据边长=1=2=..N一直扩下去，所以是O(N^2 * N) = O(N^3)
也就是说大流程是
for() { //限定边长
  for() { //遍历i
    for(){ //遍历j
       //验证边长是否是1，达到正方形 : 只有这一环节是有优化空间的
    }
  }
}

通过创建辅助数组，遍历两次数组得到,每个点往右有几个1的二维数组,往下有几个点的二维数组
时间复杂度2 * O(N^2)
而上面验证长方形可以通过这个辅助数组快速验证O(1)
在总次数是O(N^3)面前，有多少个O(N^2)都是被忽略的，所以总代价还是O(N^3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
//计算right down数组
public static void setBorderMap(int[][] m, int[][] right, int[][] down) {
    int r = m.length;
    int c = m[0].length;
    if (m[r - 1][c - 1] == 1) {
        right[r - 1][c - 1] = 1;
        down[r - 1][c - 1] = 1;
    }
    for (int i = r - 2; i != -1; i--) {
        if (m[i][c - 1] == 1) {
            right[i][c - 1] = 1;
            down[i][c - 1] = down[i + 1][c - 1] + 1;
        }
    }
    for (int i = c - 2; i != -1; i--) {
        if (m[r - 1][i] == 1) {
            right[r - 1][i] = right[r - 1][i + 1] + 1;
            down[r - 1][i] = 1;
        }
    }
    for (int i = r - 2; i != -1; i--) {
        for (int j = c - 2; j != -1; j--) {
            if (m[i][j] == 1) {
                right[i][j] = right[i][j + 1] + 1;
                down[i][j] = down[i + 1][j] + 1;
            }
        }
    }
}

//定义边长，三个循环
public static int getMaxSize(int[][] m) {
    int[][] right = new int[m.length][m[0].length];
    int[][] down = new int[m.length][m[0].length];
    setBorderMap(m, right, down); // O(N^2); + 

    for (int size = Math.min(m.length, m[0].length); size != 0; size--) {
        if (hasSizeOfBorder(size, right, down)) {
            return size;
        }
    }
    return 0;
}

public static boolean hasSizeOfBorder(int size, int[][] right, int[][] down) {
    for (int i = 0; i != right.length - size + 1; i++) {
        for (int j = 0; j != right[0].length - size + 1; j++) {
            if (right[i][j] >= size && down[i][j] >= size
                && right[i + size - 1][j] >= size
                && down[i][j + size - 1] >= size) {
                return true;
            }
        }
    }
    return false;
}
1
2
3
给定一个正整数M，请构造出一个长度为M的数组arr，要求
对任意的i、j、k三个位置，如果i<j<k，都有arr[i] + arr[k] != 2*arr[j]
返回构造出的arr
1
2
3
4
5
思想：
数组长长度小于3，都达标
把数组划分成左右两部分，挑选三个奇数不满足a + c != 2b，则(2a-1) + (2c-1) != 2b-1，成倍扩张
偶数也是同理， a + c != 2b，则2a + 2c != 4b
将M长度划分成 (M+1)/2的两份数组，左边奇数右边偶数，任意三个基数、三个偶数或者基偶结合，都达标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 生成长度为size的达标数组
// 达标：对于任意的 i<k<j，满足   [i] + [j]  != [k] * 2
public static int[] makeNo(int size) {
    if (size == 1) {
        return new int[] { 1 };
    }
    // size
    // 一半长达标来
    // 7   :   4
    // 8   :   4
    // [4个奇数] [3个偶]
    int halfSize = (size + 1) / 2;
    int[] base = makeNo(halfSize);
    // base -> 等长奇数达标来
    // base -> 等长偶数达标来
    int[] ans = new int[size];
    int index = 0;
    for(; index < halfSize;index++) {
        ans[index] = base[index] * 2 + 1;
    }
    for(int i = 0 ;index < size;index++,i++) {
        ans[index] = base[i] * 2; 
    }
    return ans;
}
1
2
3
4
5
给定一个二叉树的头节点head，路径的规定有以下三种不同的规定：

1）路径必须是头节点出发，到叶节点为止，返回最大路径和
2）路径可以从任何节点出发，但必须往下走到达任何节点，返回最大路径和
3）路径可以从任何节点出发，到任何节点，返回最大路径和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//问题1：
public static int maxDis(Node head) {
    if (head == null) {
        return 0;
    }
    return process2(head);
}

// x为头的整棵树上，最大路径和是多少，返回。
// 路径要求，一定从x出发，到叶节点，算做一个路径
//叶子节点做baseCase，因为null节点返回0可能会干扰答案
public static int process2(Node x) {
    if (x.left == null && x.right == null) {
        return x.value;
    }
    int next = Integer.MIN_VALUE;
    if (x.left != null) {
        next = process2(x.left);
    }
    if (x.right != null) {
        next = Math.max(next, process2(x.right));
    }
    return x.value + next;
}
1
2
3
4
5
6
7
第二问思路：
二叉树的递归套路
1.与X有关
2.与X无关

与X有关需要左右数提供什么信息，与X无关需要左右树提供什么信息？
有关：以左/右树开头的整数最大和   无关：左/右树的整树最大和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public static class Info {
    public int allTreeMaxSum;
    public int fromHeadMaxSum;

    public Info(int all, int from) {
        allTreeMaxSum = all;
        fromHeadMaxSum = from;
    }
}

// 1）X无关的时候， 1， 左树上的整体最大路径和 2， 右树上的整体最大路径和
// 2) X有关的时候 3， x自己 4， x往左走 5，x往右走
public static Info f2(Node x) {
    if (x == null) {
        return null;
    }
    Info leftInfo = f2(x.left);
    Info rightInfo = f2(x.right);
    int p1 = Integer.MIN_VALUE;
    if (leftInfo != null) {
        p1 = leftInfo.allTreeMaxSum;
    }
    int p2 = Integer.MIN_VALUE;
    if (rightInfo != null) {
        p2 = rightInfo.allTreeMaxSum;
    }
    int p3 = x.value;
    int p4 = Integer.MIN_VALUE;
    if (leftInfo != null) {
        p4 = x.value + leftInfo.fromHeadMaxSum;
    }
    int p5 = Integer.MIN_VALUE;
    if (rightInfo != null) {
        p5 = x.value + rightInfo.fromHeadMaxSum;
    }
    int allTreeMaxSum = Math.max(Math.max(Math.max(p1, p2), p3), Math.max(p4, p5));
    int fromHeadMaxSum = Math.max(Math.max(p3, p4), p5);
    return new Info(allTreeMaxSum, fromHeadMaxSum);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//第三问：
// 1）X无关的时候， 1， 左树上的整体最大路径和 2， 右树上的整体最大路径和
// 2) X有关的时候 3， x自己 4， x往左走 5，x往右走 6, 既往左，又往右
public static Info f3(Node x) {
    if (x == null) {
        return null;
    }
    Info leftInfo = f3(x.left);
    Info rightInfo = f3(x.right);
    int p1 = Integer.MIN_VALUE;
    if (leftInfo != null) {
        p1 = leftInfo.allTreeMaxSum;
    }
    int p2 = Integer.MIN_VALUE;
    if (rightInfo != null) {
        p2 = rightInfo.allTreeMaxSum;
    }
    int p3 = x.value;
    int p4 = Integer.MIN_VALUE;
    if (leftInfo != null) {
        p4 = x.value + leftInfo.fromHeadMaxSum;
    }
    int p5 = Integer.MIN_VALUE;
    if (rightInfo != null) {
        p5 = x.value + rightInfo.fromHeadMaxSum;
    }

    int p6 = Integer.MIN_VALUE;
    if (leftInfo != null && rightInfo != null) {
        p6 = x.value + leftInfo.fromHeadMaxSum + rightInfo.fromHeadMaxSum;
    }

    int allTreeMaxSum = Math.max(Math.max(Math.max(p1, p2), p3), Math.max(Math.max(p4, p5), p6));
    int fromHeadMaxSum = Math.max(Math.max(p3, p4), p5);
    return new Info(allTreeMaxSum, fromHeadMaxSum);
}
1
2
3
4
5
6
7
8
9
10
在行也有序、列也有序的二维数组中，找num，找到返回true，否则false

思想：
从右上角（或者左下角）开始走，匹配num，往左走遇到对不上了，就往下走，重复之前的操作
如：
1 2 3   13  16  20    
2 3 4   14  17  21
3 4 15  17  18  22

找到15的位置: 20->16->17->18->17->15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static boolean isContains(int[][] matrix, int K) {
    int row = 0;
    int col = matrix[0].length - 1;
    while (row < matrix.length && col > -1) {
        if (matrix[row][col] == K) {
            return true;
        } else if (matrix[row][col] > K) {
            col--;
        } else {
            row++;
        }
    }
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
有n个打包机器从左到右一字排开，上方有一个自动装置会抓取一批放物品到每个打包机上
放到每个机器上的这些物品数量有多有少，由于物品数量不相同，需要工人将每个机器上的物品进行移动从而到达物品数量相等才能打包。
每个物品重量太大、 每次只能搬一个物品进行移动，为了省力，只在相邻的机器上移动。
请计算在搬动最 小轮数的前提下，使每个机器上的物品数量相等。
如果不能使每个机器上的物品相同， 返回-1。 
例如[1,0,5]表示有3个机器，每个机器上分别有1、0、5个物品
经过这些轮后: 
第一轮:1    0 <- 5 => 1 1 4
第二轮:1 <- 1 <- 4 => 2 1 3
第三轮:2    1 <- 3 => 2 2 2 
移动了3轮，每个机器上的物品相等，所以返回3
例如[2,2,3]表示有3个机器，每个机器上分别有2、2、3个物品，
这些物品不管怎么移动，都不能使三个机器上物品数量相等，返回-1
1
2
3
4
5
6
7
8
9
10
思路：
机器物品数量总和 %N != 0,必定 -1 无解
转换成以某个index做下标，划分成index左边和右边两块区域
Lsum = 左边的机器总包裹数 - 左边所需的总包裹数 ?> 0 ，表示左边的机器数量过多，同理右边也是
若左右两边Lsum和Rsum均小于0，则表示index下标的机器必定有多余包裹，则移动次数 = abs(Lsum) + abs(Rsum)
其他情况均是max(abs(Lsum), abs(Rsum))

最后演变成以i结尾，求左边的累加和，右边的累加和，做计算
先遍历得到总物品数sum，每次遍历i进行左边累加和计算，右边累加和通过sum - 左边累加和得到
整体时间复杂度O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public static int MinOps(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int size = arr.length;
    int sum = 0;
    for (int i = 0; i < size; i++) {
        sum += arr[i];
    }
    if (sum % size != 0) {
        return -1;
    }
    int avg = sum / size;
    int leftSum = 0;
    int ans = 0;
    // 每个位置都求各自的
    for (int i = 0; i < arr.length; i++) {
        // i号机器，是中间机器，左(0~i-1) i 右(i+1~N-1)
        // 负 需要输入     正需要输出 
        int leftRest = leftSum - i * avg; // a-b
        // 负 需要输入     正需要输出 
        // c - d
        int rightRest =  (sum - leftSum - arr[i]) -  (size - i - 1) * avg; 
        if (leftRest < 0 && rightRest < 0) {
            ans = Math.max(ans, Math.abs(leftRest) + Math.abs(rightRest));
        } else {
            ans = Math.max(ans, Math.max(Math.abs(leftRest), Math.abs(rightRest)));
        }
        leftSum += arr[i];
    }
    return ans;
}
1
2
3
给定一个数组arr长度为N，你可以把任意长度大于0且小于N的前缀作为左部分，剩下的 作为右部分。

但是每种划分下都有左部分的最大值和右部分的最大值，请返回最大的， 左部分最大值减去右部分最大值的绝对值。
1
2
3
4
思想：
找到数组中的最大值Max，然后看0和N-1哪个值比较小，Max - 那个较小的数就是答案
因为Max最终肯定会划分在某个区间上，问题将转换成如何找到另一个不包含Max的区间内的最大值（但实际上需要尽量让这个值越小越好）
由于区间一定会包含0或者N-1的值，那么就让0或者N-1变成这个区间的最大值，因为必定包含它这个值
1
2
3
4
5
6
7
public static int maxABS3(int[] arr) {
    int max = Integer.MIN_VALUE;
    for (int i = 0; i < arr.length; i++) {
        max = Math.max(arr[i], max);
    }
    return max - Math.min(arr[0], arr[arr.length - 1]);
}

单调性

1
2
3
4
5
6
7
给定一个数组arr，已知其中所有的值都是非负的，将这个数组看作一个容器， 请返回容器能装多少水
比如，arr = {3，1，2，5，2，4}，根据值画出的直方图就是容器形状，该容 器可以装下5格水
再比如，arr = {4，5，1，3，2}，该容器可以装下2格水
例如：求水从天上落下来根据这些高度，它能盛多少格子水
        |
|水   水 |
|   |   |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
思路：
解法一：
就看i位置，求i位置左max和右max，水能盛的高度绝对不会超过min(左max，右max) - arr[i]
而且i位置过高，也无法盛水，所以是 i位置盛水的格子数 ：max(min(左max,右max) - i,0)

求i左右两边的max：
如[1,3,2,5,5,6,3]
建立辅助数组L只增不降:[1,3,3,5,5,6,6]，这样能求出[0,i]位置上，最左边的max是多少
反之，反过来从N-1开始遍历到0，能求出数组R，在[i,N-1]上的右边Max

解法二：
不使用辅助数组，采用双指针操作
例子：6 3 2 4 2 6 8
已知i = 0 和 i = N - 1 势必是不能储存水量的，所以最左右两边必然为0
采用双指针法，L = 1,R = N - 2开始
若L左边的Max < R右边的Max：
  arr[L] = 3,左Max = 6,右Max = 8
  对于L位置来说，它最多储存 6-3 格水，L = 1的位置答案 = 3，L++
若L左边的Max > R右边的Max：
  对于arr[R]位置来说，它左边有个大于右边Max的值，最多储存右Max - arr[R]格子， R++
若L左边的Max = R右边的Max：
  可以直接结算两边的结果，因为都一样，L++,R++

也就是说，左Max<右Max，则结算R位置的结果，左Max>右Max，则结算L位置的结果，若相等则都结算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//解法二
public static int water4(int[] arr) {
    if (arr == null || arr.length < 2) {
        return 0;
    }
    int N = arr.length;
    int L = 1;
    int leftMax = arr[0];
    int R = N - 2;
    int rightMax = arr[N - 1];
    int water = 0;
    while (L <= R) {
        if (leftMax <= rightMax) {
            water += Math.max(0, leftMax - arr[L]);
            leftMax = Math.max(leftMax, arr[L++]);
        } else {
            water += Math.max(0, rightMax - arr[R]);
            rightMax = Math.max(rightMax, arr[R--]);
        }
    }
    return water;
}
1
2
3
4
5
6
7
如果给你一个二维数组，每一个值表示这一块地形的高度，
求整块地形能装下多少水，类似于一块盆地，中间凹下去，积水,求积水量
例子：
9 9 9 4 9 9 9
9 1 2 3 2 9 9
9 2 3 5 9 3 9
8 7 9 9 9 9 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
思路：
定义一个小根堆，存放arr[i][j]的值，并附带上i,j的位置信息
定义一个boolean[][]数组，进入过小根堆的则标记成true
定义一个Max变量，记录弹出过小根堆的最大值

先将矩阵最外层一圈添加进小根堆，因为边缘是不会有积水的，并更新boolean[][]数组
然后弹出小根堆的最小值V，从自然智慧来说，是从矩阵边缘最薄弱的地方下手，如上例子：V = 4,Max = 4
弹出value，查看自身相邻的上下左右位置，添加没有进入过小根堆的点
并结算处于value位置的储存水量：Max - value ，若大于0，则有水，若小于0，则0格水
周而复始，把各个格子的水量累加起来就是总积水量

原理：
通过边缘薄弱的地方切入，定义一个Max，其实是基于Max作为最大值，存在Max相连的一片湖
如Max = 4，则相连的湖：1,2,3,2,2,3，这些值都是基于Max做最大值来做结算，所以积水量是Max - value
若Max的值发生了变化，则相当于寻找到另外一片湖进行计算
当Max = 5，势必来到了另一处薄弱点，但是上述例子中，5附近均没有未结算过的点，所以5的湖积水= 0

那个被4个9包围的3，一定会等到小根堆中的堆顶 = 9时，弹出9，Max = 9，才能够根据上下左右的原则添加进堆中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static class Node {
    public int value;
    public int row;
    public int col;

    public Node(int v, int r, int c) {
        value = v;
        row = r;
        col = c;
    }
}

public static class NodeComparator implements Comparator<Node> {

    @Override
    public int compare(Node o1, Node o2) {
        return o1.value - o2.value;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
public static int trapRainWater(int[][] heightMap) {
    if (heightMap == null || heightMap.length == 0 || heightMap[0] == null || heightMap[0].length == 0) {
        return 0;
    }
    int N = heightMap.length;
    int M = heightMap[0].length;
    // isEnter[i][j] == true  之前进过
    //  isEnter[i][j] == false 之前没进过
    boolean[][] isEnter = new boolean[N][M];
    // 小根堆
    PriorityQueue<Node> heap = new PriorityQueue<>(new NodeComparator());

  
    //添加边缘的四条边的值到小根堆中
    for (int col = 0; col < M - 1; col++) {
        isEnter[0][col] = true;
        heap.add(new Node(heightMap[0][col], 0, col));
    }
    for (int row = 0; row < N - 1; row++) {
        isEnter[row][M - 1] = true;
        heap.add(new Node(heightMap[row][M - 1], row, M - 1));
    }
    for (int col = M - 1; col > 0; col--) {
        isEnter[N - 1][col] = true;
        heap.add(new Node(heightMap[N - 1][col], N - 1, col));
    }
    for (int row = N - 1; row > 0; row--) {
        isEnter[row][0] = true;
        heap.add(new Node(heightMap[row][0], row, 0));
    }


    int water = 0; // 每个位置的水量，累加到water上去
    int max = 0; // 每个node在弹出的时候，如果value更大，更新max，否则max的值维持不变
    while (!heap.isEmpty()) {
        Node cur = heap.poll();
        max = Math.max(max, cur.value);
        int r = cur.row;
        int c = cur.col;
        
        //把四个边添加进堆中
        if (r > 0 && !isEnter[r - 1][c]) { // 如果有上面的位置并且上面位置没进过堆
            water += Math.max(0, max - heightMap[r - 1][c]);
            isEnter[r - 1][c] = true;
            heap.add(new Node(heightMap[r - 1][c], r - 1, c));
        }
        if (r < N - 1 && !isEnter[r + 1][c]) {
            water += Math.max(0, max - heightMap[r + 1][c]);
            isEnter[r + 1][c] = true;
            heap.add(new Node(heightMap[r + 1][c], r + 1, c));
        }
        if (c > 0 && !isEnter[r][c - 1]) {
            water += Math.max(0, max - heightMap[r][c - 1]);
            isEnter[r][c - 1] = true;
            heap.add(new Node(heightMap[r][c - 1], r, c - 1));
        }
        if (c < M - 1 && !isEnter[r][c + 1]) {
            water += Math.max(0, max - heightMap[r][c + 1]);
            isEnter[r][c + 1] = true;
            heap.add(new Node(heightMap[r][c + 1], r, c + 1));
        }
    }
    return water;
}
1
2
3
给定一个有序数组arr，给定一个正数aim
1）返回累加和为aim的，所有不同二元组
2）返回累加和为aim的，所有不同三元组
1
2
3
4
5
问题一思想：
双指针，L=0，R=N-1，一起移动，一直到L==R，跳出循环
若arr[L] + arr[R] > aim，则R--
若arr[L] + arr[R] < aim，则L++
若arr[L] + arr[R] = aim，若arr[L] != arr[L -1],收集答案，这里主要是为了防止收集重复答案，L++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static void printUniquePair(int[] arr, int k) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int left = 0;
    int right = arr.length - 1;
    while (left < right) {
        if (arr[left] + arr[right] < k) {
            left++;
        } else if (arr[left] + arr[right] > k) {
            right--;
        } else { // L   +   R   =   aim
            if (left == 0 || arr[left - 1] != arr[left]) {
                System.out.println(arr[left] + "," + arr[right]);
            }
            left++;
            right--;
        }
    }
}
1
2
问题二思想：
从左往右遍历，固定三元组中的一个值=arr[i]，问题就演变成找到i的右边范围内的二元组值等于aim - arr[i]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static void printUniqueTriad(int[] arr, int k) {
    if (arr == null || arr.length < 3) {
        return;
    }
    for (int i = 0; i < arr.length - 2; i++) {
        if (i == 0 || arr[i] != arr[i - 1]) {
            printRest(arr, i, i + 1, arr.length - 1, k - arr[i]);
        }
    }
}

public static void printRest(int[] arr, int f, int l, int r, int k) {
    while (l < r) {
        if (arr[l] + arr[r] < k) {
            l++;
        } else if (arr[l] + arr[r] > k) {
            r--;
        } else {
            if (l == f + 1 || arr[l - 1] != arr[l]) {
                System.out.println(arr[f] + "," + arr[l] + "," + arr[r]);
            }
            l++;
            r--;
        }
    }
}
1
2
3
4
5
6
7
8
长度为N的数组arr，一定可以组成N^2个数值对。
例如arr = [3,1,2]，
数值对有(3,3) (3,1) (3,2) (1,3) (1,1) (1,2) (2,3) (2,1) (2,2)，
也就是任意两个数都有数值对，而且自己和自己也算数值对。
数值对怎么排序？规定，第一维数据从小到大，第一维数据一样的，第二维数组也从小到大。所以上面的数值对排序的结果为：
(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)

给定一个数组arr，和整数k，返回第k小的数值对。
1
2
3
4
5
6
7
8
9
10
思想：
假设数组是有序的,每个index 能产生N个数值对，所以总数值对是N * N
第一个数：通过(K - 1) / N 定位，假设它等于F
第二个数：假设小于F的数有A个，先减掉开头小于F的值 K - (A * N) = S
        然后假设等于F的有B个，那么以F开头，和i=0能匹配出 F * B的结果，同理i=1也有F*B个结果...
所以问题又转换以F作为第一个数值的前提下：
每个index 能产生 B个数值对，要找到第S小的数值对，所以第二个数 = (S - 1) / B

排序数组O(N*logN)，求第一个数O(1)，求第二个数也是O(1)
所以问题转换成排序上，这种求第K小的数，可以使用bfprt算法中的改写快排方法：O(N)
1
2
3
4
5
6
7
8
9
每种工作有难度和报酬，规定如下
class Job {
public int money;// 该工作的报酬
public int hard; // 该工作的难度
}
给定一个Job类型的数组jobarr，表示所有岗位，每个岗位都可以提供任意份工作
选工作的标准是在难度不超过自身能力值的情况下，选择报酬最高的岗位
给定一个int类型的数组arr，表示所有人的能力
返回int类型的数组，表示每个人按照标准选工作后所能获得的最高报酬
1
2
3
4
5
6
思想：
按工作难度从小到大排序,难度一样时钱数由大到小排序，丢弃难度相同报酬低的工作
如果难度递增的时候，报酬没递增，也丢弃
保证了剩下的序列一定是难度上升，报酬也上升的，单调性
把剩下的加入有序表，一个对象有难度, 有钱数，有序表里根据难度排序
接下来一个有能力的人在有序表里查离你的能力小于等于最近的项目，取出该项目, 获得这个钱, 一定是最值得的
1
2
3
4
背包容量为w
一共有n袋零食, 第i袋零食体积为v[i] 
总体积不超过背包容量的情况下，
一共有多少种零食放法？(总体积为0也算一种放法)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static int ways1(int[] arr, int w) {
    // arr[0...]
    return process(arr, 0, w);
}

// 从左往右的经典模型
// 还剩的容量是rest，arr[index...]自由选择，
// 返回选择方案
// index ： 0～N
// rest : 0~w
public static int process(int[] arr, int index, int rest) {
    if (rest < 0) { // 没有容量了
        // -1 无方案的意思
        return -1;
    }
    // rest>=0,
    if (index == arr.length) { // 无零食可选
        return 1;
    }
    // index号零食，要 or 不要
    // index, rest
    // (index+1, rest)
    // (index+1, rest-arr[i])
    int next1 = process(arr, index + 1, rest); // 不要
    int next2 = process(arr, index + 1, rest - arr[index]); // 要
    return next1 + (next2 == -1 ? 0 : next2);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//动态规划
//i表示index，当前背包背的体积
//i行 j列 = arr[i-1][j] + arr[i][j - arr[i-1]]
//表示自己不背的答案 + 背的答案
public static int ways3(int[] arr, int w) {
    int N = arr.length;
    int[][] dp = new int[N][w + 1];
    //j = 0,i = [0...N-1]范围上 背了0个零食的答案
    for (int i = 0; i < N; i++) {
        dp[i][0] = 1;
    }
    //i = 0, j = [0..w]背了1号零食的答案
    if (arr[0] <= w) {
        dp[0][arr[0]] = 1;
    }
    for (int i = 1; i < N; i++) {
        for (int j = 1; j <= w; j++) {
            dp[i][j] = dp[i - 1][j] + ((j - arr[i]) >= 0 ? dp[i - 1][j - arr[i]] : 0);
        }
    }
    int ans = 0;
    //求二维数组中最后一行的累加答案
    for (int j = 0; j <= w; j++) {
        ans += dp[N - 1][j];
    }
    return ans;
}

空间压缩

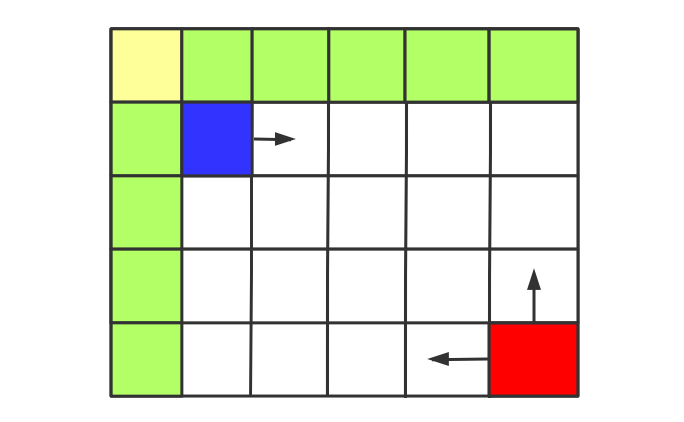
algorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
黄色：已知的点对应的值
红色：答案所在的点
假设arr[i][j]答案需要依赖 arr[i - 1][j] 和 arr[i][j - 1]
那么根据已知的点，可以求出 arr[0][j]第一排的答案

空间压缩：
空间压缩是指将二维数组的空间压缩成一维数组的空间
通过计算得到一行或者一列的结果，存放到一位数组中
准备计算下一行或者下一列的结果时，通过值覆盖的方式，将答案填回一维数组

若有arr[i][j]依赖了arr[i-1][j-1]的结果，可以通过使用一个临时变量存储arr[i-1][j-1]的结果。

若有arr[i][j]依赖了之前几行的数据，可以申请几个一位数组，交替覆盖。
1
2
3
4
5
给定两个字符串str1和str2，求两个字符串的最长公共子串
请注意区分子串和子序列的不同：
子串表示连续的字符串,子序列可以不连续

动态规划的空间压缩技巧！
1
2
3
4
5
6
7
8
9
10
11
思想：
简历动态规划的二维表
行：[0...M-1] M是str1的长度
列：[0...N-1] N是str2的长度
值：arr[i][j] = str1中必须以j位置结尾，且str2中必须以i位置结尾的最长公共子串长度
所以两个最长公共子串就是二维表中的Max值

arr[i][j] 依赖 str2[j] ?= str1[i] 和arr[i-1][j-1]
它只依赖二维表中的一个值，
等同于起点位于右上角，然后一条从左往右的斜线一直在计算[i-1,j-1]、[i,j]、[i+1,j+1]的值
也就是说，可以通过有限几个变量计算结果，而不需要申请二维表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//动态规划 + 空间压缩！！！
public static String lcst2(String str1, String str2) {
    if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
        return "";
    }
    char[] chs1 = str1.toCharArray();
    char[] chs2 = str2.toCharArray();
    int row = 0; // 出发点的行号
    int col = chs2.length - 1; // 出发点的列号
    int max = 0;
    //str1的最长子串的结束下标
    int end = 0;
    //出发的起点在右上角
    while (row < chs1.length) {
        int i = row;
        int j = col;
        //缓存arr[i-1][j-1]的答案
        int len = 0;
        // 向右下方移动的这一轮
        while (i < chs1.length && j < chs2.length) {
            //若不等，则为0
            if (chs1[i] != chs2[j]) {
                len = 0;
            } else {
                //若相等，则根据上一次求的答案arr[i][j] = arr[i-1][j-1] + 1 
                len++;
            }
            //若有长度超过Max，则更新，并记录str1的最长公共子串末尾下标
            if (len > max) {
                end = i;
                max = len;
            }
            //往右下对角线移动
            i++;
            j++;
        }
        //行号--,一直往左移动，移动到不能往左了，就列号++,往下移动
        if (col > 0) {
            col--;
        } else {
            row++;
        }
    }
    //公共子串末尾index - max + 1则是公共子串的开头第一个字符！截取返回
    return str1.substring(end - max + 1, end + 1);
}
1
2
3
给定一个由字符串组成的数组String[] strs，给定一个正数K
返回词频最大的前K个字符串，假设结果是唯一的
如：["abc","ab","abc","aaaa","ab","abc"]   K=2 -> return "abc" 和 "ab"
1
2
3
4
5
6
7
思路：
用HashMap<String,Integer>统计每个字符串的词频，然后使用小根堆做资源限制条件
维持小根堆的大小=K ，把HashMap的数据添加到小根堆中
堆顶就是门槛，当词频数大于堆顶，则弹出堆顶，并添加新对象，周而复始，小根堆留着的，肯定是词最大K个频数

解法二：
统计词频后，可以用改进的快排，求出第K大的数，时间复杂度O(N)，用小根堆是O(N*logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static class Node {
    public String str;
    public int times;

    public Node(String s, int t) {
        str = s;
        times = t;
    }
}

public static class NodeComparator implements Comparator<Node> {

    @Override
    public int compare(Node o1, Node o2) {
        return o1.times - o2.times;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static void printTopKAndRank(String[] arr, int topK) {
    if (arr == null || arr.length == 0 || topK < 1 || topK > arr.length) {
        return;
    }
    HashMap<String, Integer> map = new HashMap<>();
    for (String str : arr) {
        if (!map.containsKey(str)) {
            map.put(str, 1);
        } else {
            map.put(str, map.get(str) + 1);
        }
    }
    PriorityQueue<Node> heap = new PriorityQueue<>(new NodeComparator());
    for (Entry<String, Integer> entry : map.entrySet()) {
        Node cur = new Node(entry.getKey(), entry.getValue());
        //如果没满，加进去
        if (heap.size() < topK) {
            heap.add(cur);
        } else {
            //满了，判断堆顶和cur哪个大
            if (heap.peek().times < cur.times) {
                heap.poll();
                heap.add(cur);
            }
        }
    }
    while (!heap.isEmpty()) {
        System.out.println(heap.poll().str);
    }
}
1
2
3
4
5
6
7
8
9
请实现如下结构：
TopRecord{
public TopRecord(int K)  :  构造时事先指定好K的大小，构造后就固定不变了
public  void add(String str)  :   向该结构中加入一个字符串，可以重复加入
public  List<String> top() : 返回之前加入的所有字符串中，词频最大的K个
}
要求： 
add方法，复杂度O(log K);
top方法，复杂度O(K)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//自定义的堆结构
public static class TopKRecord {
    private Node[] heap;
    //小根堆的大小下标
    private int heapSize;
    // 字符串对应的词频
    private HashMap<String, Node> strNodeMap;
    //小根堆上的节点所在的index位置
    private HashMap<Node, Integer> nodeIndexMap;

    public TopKRecord(int K) {
        heap = new Node[K];
        heapSize = 0;
        strNodeMap = new HashMap<String, Node>();
        nodeIndexMap = new HashMap<Node, Integer>();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// str用户现在给我的
/*
思路：
如果str不在词频统计上，缓存词频统计，和小根堆堆顶比较
如果str在词频统计上，则词频数++，重新和小根堆堆顶比较
*/
public void add(String str) {
    Node curNode = null;
    int preIndex = -1; // str之前在堆上的位置
    // 查词频表，看看有没有关于这个str的记录
    if (!strNodeMap.containsKey(str)) { // str之前没进来过
        curNode = new Node(str, 1);
        strNodeMap.put(str, curNode);
        nodeIndexMap.put(curNode, -1);
    } else { // str之前进来过
        curNode = strNodeMap.get(str);
        curNode.times++;
        //获取字符串的index
        preIndex = nodeIndexMap.get(curNode);
    }

    // 词频表修改完毕，
    if (preIndex == -1) { // 不在堆上
        if (heapSize == heap.length) { // 堆满了
            //如果堆顶的词频数比新的词频小
            if (heap[0].times < curNode.times) {
                //交换存储的索引位置
                nodeIndexMap.put(heap[0], -1);
                nodeIndexMap.put(curNode, 0);
                //重新设置堆顶heapify下沉
                heap[0] = curNode;
                heapify(0, heapSize);
            }
        } else {// 堆没有满
            nodeIndexMap.put(curNode, heapSize);
            heap[heapSize] = curNode;
            //尾部插入，heapInsert上浮
            heapInsert(heapSize++);
        }
    } else { // str已经在堆上了
        heapify(preIndex, heapSize);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
private void heapify(int index, int heapSize) {
    int l = index * 2 + 1;
    int r = index * 2 + 2;
    int smallest = index;
    //不能越界超过heapSize
    while (l < heapSize) {
        if (heap[l].times < heap[index].times) {
            smallest = l;
        }
        if (r < heapSize && heap[r].times < heap[smallest].times) {
            smallest = r;
        }
        if (smallest != index) {
            swap(smallest, index);
        } else {
            break;
        }
        index = smallest;
        l = index * 2 + 1;
        r = index * 2 + 2;
    }
}

private void swap(int index1, int index2) {
    nodeIndexMap.put(heap[index1], index2);
    nodeIndexMap.put(heap[index2], index1);
    Node tmp = heap[index1];
    heap[index1] = heap[index2];
    heap[index2] = tmp;
}
1
2
3
4
5
6
7
8
9
10
11
12
给你一个字符串类型的数组arr，譬如:
String[] arr = { "b\st", "d\", "a\d\e", "a\b\c" }; 
把这些路径中蕴含的目录结构给打印出来，子目录直接列在父目录下面，并比父目录向右进两格，就像这样:
a
  b
    c
  d
    e
b
  st
d
同一级的需要按字母顺序排列不能乱。
1
2
思想：
把路径变成前缀树形式，并且使用TreeMap排序前缀树，最后深度优先遍历输出，格子的数量：2 * (层数 - 1)
1
2
3
4
5
6
7
8
9
10
11
public static class Node {
    // 上一个节点是通过哪条路，到我的
    public String path;
    // key : node下级的路   value：node在key这条路上对应的节点是什么
    public TreeMap<String, Node> nextMap;

    public Node(String p) {
        this.path = p;
        nextMap = new TreeMap<>();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// folderPaths ->  [   "a\b\c","a\b\s" , "a\d\e" ,"e\f\sty"     ]
public static void print(String[] folderPaths) {
    if (folderPaths == null || folderPaths.length == 0) {
        return;
    }
    // 根据所有字符串，把前缀树建立好，头节点为head
    Node head = generateFolderTree(folderPaths);

    // 打印
    printProcess(head, 0);
}

public static Node generateFolderTree(String[] folderPaths) {
    Node head = new Node(""); // 系统根目录, 前缀树头节点
    for (String foldPath : folderPaths) { // 拿出每一个绝对路径
        String[] paths = foldPath.split("\\\\"); // java 特性，用一个"\"做分割的意思
        Node cur = head;
        for (int i = 0; i < paths.length; i++) { // "a"  , "b"   ,"c"
            if (!cur.nextMap.containsKey(paths[i])) {
                cur.nextMap.put(paths[i], new Node(paths[i]));
            }
            cur = cur.nextMap.get(paths[i]);
        }
    }
    return head;
}

// head节点，当前在level层
public static void printProcess(Node node, int level) {
    if (level != 0) {
        // 2 * (level - 1)
        System.out.println(get4nSpace(level) + node.path);
    }
    for (Node next : node.nextMap.values()) {
        printProcess(next, level + 1);
    }
}

public static String get4nSpace(int n) {
    String res = "";
    for (int i = 1; i < n; i++) {
        res += "    ";
    }
    return res;
}
1
2
3
4
5
已知一棵二叉树中没有重复节点，并且给定了这棵树的中序遍历数组和先序遍历 数组，返回后序遍历数组。
比如给定:
int[] pre = { 1, 2, 4, 5, 3, 6, 7 };
int[] in = { 4, 2, 5, 1, 6, 3, 7 }; 
返回:{4,5,2,6,7,3,1}
1
2
3
4
5
6
7
8
9
10
11
思路：
先序：头左右 
中序：左头右 
后序：左右头

所以先序的第一个头位置，一定是后序的最后一个头位置
然后去中序列表，寻找头的位置，中序左边的部分是左树L，右边的部分是右树R
以先序的头index + 1则是左树开始的LL
以LL + 中序算出来的左树长度 L ，这部分，就会放在后序的左部分

递归计算每个树的位置放到后序数组中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public static int[] preInToPos2(int[] pre, int[] in) {
    //若两段长度不同，则直接范围
    if (pre == null || in == null || pre.length != in.length) {
        return null;
    }
    int N = pre.length;
    //先缓存中序中，每个数值对应的i位置，方便计算
    HashMap<Integer, Integer> inMap = new HashMap<>();
    for (int i = 0; i < N; i++) {
        inMap.put(in[i], i);
    }
    int[] pos = new int[N];
    
    process2(pre, 0, N - 1, in, 0, N - 1, pos, 0, N - 1, inMap);
    return pos;
}
/*
L1..R1 是pre数组范围
L2..R2 是in 数组范围
L3..R3 是pos数组范围
*/
public static void process2(int[] pre, int L1, int R1, int[] in, int L2, int R2, int[] pos, int L3, int R3,
                            HashMap<Integer, Integer> inMap) {
    if (L1 > R1) {
        return;
    }
    //如果只有一个数，则直接设置
    if (L1 == R1) {
        pos[L3] = pre[L1];
        return;
    }
    //将先序的头L1位置 放到后序的末尾R3位置
    pos[R3] = pre[L1];
    //查询头L1在中序中的index，将左右树根据这个中心头节点，划分成左右两块不同的区域
    int mid = inMap.get(pre[L1]);
    //该头节点的左树的长度等于 index - L2
    int leftSize = mid - L2;
    //递归计算左区域的结果
    process2(pre, L1 + 1, L1 + leftSize, in, L2, mid - 1, pos, L3, L3 + leftSize - 1, inMap);
    
    //递归计算右区域的结果
    process2(pre, L1 + leftSize + 1, R1, in, mid + 1, R2, pos, L3 + leftSize, R3 - 1, inMap);
}
1
2
最长递增子序列问题的O(N*logN)的解法
最长递增子序列：{3,1,4,2,3} --> {1,2,3}严格递增，不能相等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
O(N^2) 解法：
动态规划，一维数组dp，以每个i位置为下标，value存储以i位置结尾的最长递增子序列长度
通过查看i位置左边比他小的值，取其中递增子序列的max最大值 + 1

O(N * logN) 解法：
增加一个ends数组，end[i]=V，其中V表示arr数组中，最长递增子序列 = i + 1 时的序列结尾的最小值
当计算以i结尾的最长子序列长度时，通过二分找ends数组中，大于等于arr[i]的最左位置
若无结果，则将arr[i]插入到ends中
若有结果，假设其下标在ends数组中是k,则将ends[k]的值更新成arr[i]
那么，dp[i]的值就是k + 1,有k + 1个最长子序列

如：
     {3,1,4,2,3,7...} --> {1,2,3,7...}
dp:  {1} -> {1,1} ->{1,1,2} -> {1,1,2,2} -> {1,1,2,2,3} -> ...
ends:{3} -> {1}   ->{1,4}   -> {1,2}     -> {1,2,3}     -> ...

假设遍历了5次，i从0开始，这时候i = 4，
根据例子可以看到，ends[2] = 3 = arr[4], 最长递增子序列 dp[4] = 2(ends的index) + 1 = 3
也就是代表着 从下标[0..4]内，在最长递增子序列的长度都 = 3时的min(arr[i]) = 3
如{1,2,3}和{1,2,7},长度为3的最长递增子序列的最小结尾 = 3

ends数组可以保证有序，因为当最长子序列长度相同时，min(arr[i])一定是相同的，只有长度增加时，它的值才会变化，而且当长度上升时，其对应的值必定 > min(arr[i])

遍历arr数组，时间复杂度O(N)， 遍历过程中计算dp数组采用了ends数组，ends长度为N
ends数组中通过二分查找大于arr[i]中的最左位置 O(logN)
所以整体的时间复杂度是O(N * logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//O(N * logN)
//构建dp数组
public static int[] getdp2(int[] arr) {
    int[] dp = new int[arr.length];
    int[] ends = new int[arr.length];
    ends[0] = arr[0];
    dp[0] = 1;
    int right = 0; // 0....right   right往右无效
    int l = 0;
    int r = 0;
    int m = 0;
    for (int i = 1; i < arr.length; i++) {
        //二分，找ends数组中，大于等于arr[i]的最左的位置
        l = 0;
        r = right;
        while (l <= r) {
            m = (l + r) / 2;
            if (arr[i] > ends[m]) {
                l = m + 1;
            } else {
                r = m - 1;
            }
        }
        //若有效区没找到，需要扩充有效区，则l = right+1  right需要扩容更新值
        //若有效区找到了，则l < right， right需要原值 
        //取两者的max
        right = Math.max(right, l);
        //更新ends的值，把大于等于arr[i]的最左的位置更新成arr[i]
        ends[l] = arr[i];
        //赋值dp值
        dp[i] = l + 1;
    }
    return dp;
}
1
2
每个信封都有长和宽两个维度的数据，A信封如果想套在B信封里面，A信封必须在长和宽上都小于B信封才行。
如果给你一批信封，返回最大的嵌套层数
1
2
3
4
思路：
先排序第一维数据(长度)由小到大，如果第一维一样, 第二维数据(宽度)由大到小
第二维度数据单独拎出来, 它的最长递增子序列就是套的层数
因为长度已经先排好序了，若宽度也按照递增子序列递增，那么保证了长也递增，宽也递增，那么答案就出来了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static class Envelope {
    public int l;
    public int h;

    public Envelope(int weight, int hight) {
        l = weight;
        h = hight;
    }
}

public static class EnvelopeComparator implements Comparator<Envelope> {
    @Override
    public int compare(Envelope o1, Envelope o2) {
        return o1.l != o2.l ? o1.l - o2.l : o2.h - o1.h;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static Envelope[] getSortedEnvelopes(int[][] matrix) {
    Envelope[] res = new Envelope[matrix.length];
    for (int i = 0; i < matrix.length; i++) {
        res[i] = new Envelope(matrix[i][0], matrix[i][1]);
    }
    Arrays.sort(res, new EnvelopeComparator());
    return res;
}

public static int maxEnvelopes(int[][] matrix) {
    Envelope[] envelopes = getSortedEnvelopes(matrix);
    int[] ends = new int[matrix.length];
    ends[0] = envelopes[0].h;
    int right = 0;
    int l = 0;
    int r = 0;
    int m = 0;
    for (int i = 1; i < envelopes.length; i++) {
        l = 0;
        r = right;
        while (l <= r) {
            m = (l + r) / 2;
            if (envelopes[i].h > ends[m]) {
                l = m + 1;
            } else {
                r = m - 1;
            }
        }
        right = Math.max(right, l);
        ends[l] = envelopes[i].h;
    }
    return right + 1;
}
1
给定一个数组arr，返回子数组的最大累加和。
1
2
3
4
思路：
定义一个cur和一个max的变量
cur进行数据的累加，并赋值给max，若下次累加大于max，则更新max的值
若累加的值小于0，则放弃之前的累加和，从0开始重新计算，重置成0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int maxSum(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int max = Integer.MIN_VALUE;
    int cur = 0;
    for (int i = 0; i != arr.length; i++) {
        cur += arr[i];
        max = Math.max(max, cur);
        //累加和小于0，则重置成0
        cur = cur < 0 ? 0 : cur;
    }
    return max;
}
1
给定一个整型矩阵，返回子矩阵的最大累加和。
1
2
3
4
5
6
7
8
9
10
思想：
求[0~0]...[0~1]...[0~N-1]行的最大累加和
再求[1~1]..[1~2]...[1~N-1]行的最大累加和
以此类推，最终最大的累加和答案就出来了
而求[0~0]行的最大累加和，等于求一维数组的最大累加和
而求[0~1]行的最大累加和，通过将[0~0]行的数组,按照相同列，进行累加，累加到[0~1]行中，最后还是一维数组
这就是数组压缩技巧

时间复杂度O(N^2 * M)
N是行，M是列，挑选小的值做行，常数项优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static int maxSum(int[][] m) {
    if (m == null || m.length == 0 || m[0].length == 0) {
        return 0;
    }
    int max = Integer.MIN_VALUE;
    int cur = 0;
    int[] s = null;
    //遍历数组的每行
    for (int i = 0; i != m.length; i++) { // 开始的行号i
        //累加每行
        s = new int[m[0].length]; 
        //遍历数组的每列 
        for (int j = i; j != m.length; j++) { // 结束的行号j，i~j行是我讨论的范围
            
            //计算一维数组累加和
            cur = 0;
            for (int k = 0; k != s.length; k++) {
                s[k] += m[j][k];
                cur += s[k];
                max = Math.max(max, cur);
                cur = cur < 0 ? 0 : cur;
            }
        }
    }
    return max;
}
1
2
3
双向链表节点结构和二叉树节点结构是一样的，如果你把last认为是left，next认为是right的话。
给定一个搜索二叉树的头节点head，请转化成一条有序的双向链表，并返回链表的头节点。
链表中的顺序以中序遍历排列
1
2
3
4
5
6
7
8
9
10
// 整棵树，串成双向链表，返回头、尾
public static class Info {
    public Node start;
    public Node end;

    public Info(Node start, Node end) {
        this.start = start;
        this.end = end;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 以x为头的整棵搜索二叉树，请全部以有序双向链表的方式，连好
// 并且返回，整个有序双向链表的头节点和尾节点
public static Info process(Node X) {
    if (X == null) {
        return new Info(null, null);
    }
    Info leftInfo = process(X.left);
    Info rightInfo = process(X.right);	
    if (leftInfo.end != null) {
        leftInfo.end.right = X;
    }
    X.left = leftInfo.end;
    X.right = rightInfo.start;
    if (rightInfo.start != null) {
        rightInfo.start.left = X;
    }
    return new Info(
        // 整棵树的头，
        leftInfo.start != null ? leftInfo.start : X
        ,
        // 整棵树的尾
        rightInfo.end != null ? rightInfo.end : X);
}

编辑距离

1
2
3
4
5
给定两个字符串str1和str2，再给定三个整数ic、dc和rc，分别代表插入、删除和替换一个字符的代价，返回将str1编辑成str2的最小代价。
【举例】
str1="abc"，str2="adc"，ic=5，dc=3，rc=2 从"abc"编辑成"adc"，把'b'替换成'd'是代价最小的，所以返回2 
str1="abc"，str2="adc"，ic=5，dc=3，rc=100 从"abc"编辑成"adc"，先删除'b'，然后插入'd'是代价最小的，所以返回8
str1="abc"，str2="abc"，ic=5，dc=3，rc=2 不用编辑了，本来就是一样的字符串，所以返回0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
思路：
二维表的范围尝试模型的动态规划问题，一个字符串做行，一个字符串做列的二维数组dp
dp[i][j]的含义是 str1拿出前缀为i的长度和str2前缀为j的长度的最小编辑代价

dp[0][0] = 0
dp数组的第0行：以str1拿出0个字符，变成[0...N-1]的代价，则是dp[0][j] = j * rc,字符长度多少，就多少个插入代价
dp数组的第0列：以str1拿出[0...N-1]个字符，变成0个字符的代价，则是dp[i][0] = i * dc，字符长度多少，多少个删除代价

四种情况：
一：dp[i][j] = dp[i-1][j-1] + rc 如果str1[i] != str2[j]，直接将i字符替换成j字符，一个替换字符的代价
二：dp[i][j] = dp[i-1][j-1] + 0 如果str1[i] == str2[j]，替换代价 = 0
三：将str1部分前缀变成str2，然后删除str1后缀中的多余的字符
四：将str1整体字符变成str2的前缀字符，然后添加str2未匹配的后缀字符

分大类:
保留str1的i字符：
  i位置作为j位置的字符 ：str1[i] ?= str[j]
     == : 0个代价
     != : 一个替换代价
  i位置不作为j位置的字符：作为str2的前缀字符,然后添加j字符
不保留str1的i字符：
  删除i字符，将[0,i-1]字符变成str2
  
时间复杂度O(N * M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static int minCost1(String s1, String s2, int ic, int dc, int rc) {
    if (s1 == null || s2 == null) {
        return 0;
    }
    char[] str1 = s1.toCharArray();
    char[] str2 = s2.toCharArray();
    //N M 是dp中的字符串长度映射的index，而不是下标对下标
    int N = str1.length + 1;
    int M = str2.length + 1;
    int[][] dp = new int[N][M];
    // dp[0][0]  = 0 ，字符串长度为0时，成倍的新增和删除的代价
    for (int i = 1; i < N; i++) {
        dp[i][0] = dc * i;
    }
    for (int j = 1; j < M; j++) {
        dp[0][j] = ic * j;
    }
    for (int i = 1; i < N; i++) {
        for (int j = 1; j < M; j++) {
            //如果末位字符相同，则0个替换代价，否则添加一个替换代价
            if (str1[i - 1] == str2[j - 1]) {
                //情况一：如果末位字符相同,等于大家都少选一个长度的代价
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                //情况二：增加一个替换代价
                dp[i][j] = dp[i - 1][j - 1] + rc;
            }
            //情况三：保留i字符，str1变换成str2的j-1个长度，再插入一个j字符的代价
            dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + ic);
            //情况四：不保留i字符，str1变换成str2的j个长度，再来个删除i字符的代价
            dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + dc);
        }
    }
    return dp[N - 1][M - 1];
}
1
2
3
给定两个字符串s1和s2，问s2最少删除多少字符可以成为s1的子串？
比如 s1 = "abcde"，s2 = "axbc"
返回1。s2删掉'x'就是s1的子串了。
1
2
3
4
5
6
7
8
思路：
解法一：
如果S2很短，则可以计算S2的所有子序列（2^M数量），M是S2的长度，然后用KMP判断哪个最长子序列是否是S1的子串
那么S2最少需要删除 M - 最长子序列长度, 时间复杂度O(N * 2^M)

解法二：
若S2很长，则S1求所有子串O(N^2)，求S1所有子串和S2的编辑距离，S1子串通过插入行为转换成S2
时间复杂度是O(N^3 * M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 解法一：
// 因为题目原本的样本数据中，有特别说明s2的长度很小。所以这么做也没有太大问题，也几乎不会超时。
// 但是如果某一次考试给定的s2长度远大于s1，这么做就不合适了。
public static int minCost1(String s1, String s2) {
    List<String> s2Subs = new ArrayList<>();
    //得到S2的所有子序列
    process(s2.toCharArray(), 0, "", s2Subs);
    //按照长度排序，优先遍历长度长的
    s2Subs.sort(new LenComp());
    for (String str : s2Subs) {
        //若匹配，则返回答案
        if (s1.indexOf(str) != -1) { // indexOf底层和KMP算法代价几乎一样，也可以用KMP代替
            return s2.length() - str.length();
        }
    }
    //若所有子序列都不匹配，则等于S2全部都要删掉
    return s2.length();
}

public static void process(char[] str2, int index, String path, List<String> list) {
    if (index == str2.length) {
        list.add(path);
        return;
    }
    process(str2, index + 1, path, list);
    process(str2, index + 1, path + str2[index], list);
}

public static class LenComp implements Comparator<String> {

    @Override
    public int compare(String o1, String o2) {
        return o2.length() - o1.length();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
// 解法二
// 枚举所有s1的子串
// 然后考察每个子串和s2的编辑距离(假设编辑距离只有删除动作且删除一个字符的代价为1)
// 如果s1的长度较小，s2长度较大，这个方法比较合适
public static int minCost2(String s1, String s2) {
    if (s1.length() == 0 || s2.length() == 0) {
        return s2.length();
    }
    int ans = Integer.MAX_VALUE;
    char[] str2 = s2.toCharArray();
    //枚举所有s1的子串
    for (int start = 0; start < s1.length(); start++) {
        for (int end = start + 1; end <= s1.length(); end++) {
            // str1[start....end]
            //假设只有插入行为，求子串和Str2的编辑距离
            ans = Math.min(ans, distance(str2, s1.substring(start, end).toCharArray()));
        }
    }
    return ans == Integer.MAX_VALUE ? s2.length() : ans;
}

// 求str2到s1sub的编辑距离
// 假设编辑距离只有删除动作且删除一个字符的代价为1
public static int distance(char[] str2, char[] s1sub) {
    int row = str2.length;
    int col = s1sub.length;
    int[][] dp = new int[row][col];
    // dp[i][j]的含义：
    // str2[0..i]仅通过删除行为变成s1sub[0..j]的最小代价
    // 可能性一：
    // str2[0..i]变的过程中，不保留最后一个字符(str2[i])，
    // 那么就是通过str2[0..i-1]变成s1sub[0..j]之后，再最后删掉str2[i]即可 -> dp[i][j] = dp[i-1][j] + 1
    // 可能性二：
    // str2[0..i]变的过程中，想保留最后一个字符(str2[i])，然后变成s1sub[0..j]，
    // 这要求str2[i] == s1sub[j]才有这种可能, 然后str2[0..i-1]变成s1sub[0..j-1]即可
    // 也就是str2[i] == s1sub[j] 的条件下，dp[i][j] = dp[i-1][j-1]
    
    //单个字符相等，则不需要删除，所以删除次数=0次
    dp[0][0] = str2[0] == s1sub[0] ? 0 : Integer.MAX_VALUE;
    //str2只有一个字符的时候，不管怎么删，都无法变成长度大于1的S1的子串
    for (int j = 1; j < col; j++) {
        dp[0][j] = Integer.MAX_VALUE;
    }
    //没相同字符，无穷大，有相同字符的话，删除的数量一定是 length - 1
    for (int i = 1; i < row; i++) {
        dp[i][0] = (dp[i - 1][0] != Integer.MAX_VALUE || str2[i] == s1sub[0]) ? i : Integer.MAX_VALUE;
    }
    for (int i = 1; i < row; i++) {
        for (int j = 1; j < col; j++) {
            dp[i][j] = Integer.MAX_VALUE;
            //利用[0,i-1]转换成[0,j]，删除i字符
            if (dp[i - 1][j] != Integer.MAX_VALUE) {
                dp[i][j] = dp[i - 1][j] + 1;
            }
            //如果i字符=j字符，删其他字符
            if (str2[i] == s1sub[j] && dp[i - 1][j - 1] != Integer.MAX_VALUE) {
                dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1]);
            }

        }
    }
    return dp[row - 1][col - 1];
}
1
2
3
4
5
解法二的优化
优化点：计算子串长度[0,1]之后，基于[0,1]的结果dp表结果，补多一行变成[0,2]的dp结果
前缀index相同时，可以共用同一张dp表，前缀index不同，无法共用
但是可以共用dp数组，以j = 0做起始列，计算整个dp数组，下次以j = 1做起始列，覆盖整个dp数组
最终会优化成O(N^2 * M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public static int minCost3(String s1, String s2) {
    if (s1.length() == 0 || s2.length() == 0) {
        return s2.length();
    }
    char[] str2 = s2.toCharArray();
    char[] str1 = s1.toCharArray();
    int M = str2.length;
    int N = str1.length;
    int[][] dp = new int[M][N];
    //M可以认为是正无穷，无效解
    int ans = M;
    //start : dp数组以哪一列做起始列
    for (int start = 0; start < N; start++) { // 开始的列数
         //单个字符相等，则不需要删除，所以删除次数=0次,否则正无穷
        dp[0][start] = str2[0] == str1[start] ? 0 : M;
        for (int row = 1; row < M; row++) {
             //没相同字符，无穷大，有相同字符的话，删除的数量一定是 row
            dp[row][start] = (str2[row] == str1[start] || dp[row - 1][start] != M) ? row : M;
        }
        //先取起始列的最后的值做答案
        ans = Math.min(ans, dp[M - 1][start]);
        // 以上已经把start列，填好
        // 以下要把dp[...][start+1....N-1]的信息填好
        //小加速：end - start 表示以start 开始，向右推了j列，当j+1 > M，则S2无法通过删除变成S1的子串
        //比如Str2长度只有10，怎么可能删除出长度12的字符呢？
        //所以end -start + 1 <= M --> end - start < M 作为for循环的加速条件
        for (int end = start + 1; end < N && end - start < M; end++) {
            
            int first = end - start;
            //这里first是表示以start做起始列时， i == j，表示str2的字符串和s1子串长度相等时的情况
            //先把等长的结果先填写，等长结果直接看最后一个字符，要么0，要么M
            dp[first][end] = (str2[first] == str1[end] && dp[first - 1][end - 1] == 0) ? 0 : M;
            
            //因为first长度>=当前dp的end - start列长度才有效，所以dp右上半空间不考虑
            //现在是end - start列固定了，所以直接计算 frist + 1
            for (int row = first + 1; row < M; row++) {
                dp[row][end] = M;
                if (dp[row - 1][end] != M) {
                    dp[row][end] = dp[row - 1][end] + 1;
                }
                if (dp[row - 1][end - 1] != M && str2[row] == str1[end]) {
                    dp[row][end] = Math.min(dp[row][end], dp[row - 1][end - 1]);
                }
            }
            ans = Math.min(ans, dp[M - 1][end]);
        }
    }
    return ans;
}
1
求完全二叉树节点的个数,要求时间复杂度低于O(N)
1
2
3
4
思想：
求以左树和右树的作为头节点的深度，进行比较
若左树深度A = 右树深度B，则左树一定是满二叉树，那么左树 + 头节点 = [2^A -1] + 1，右树递归去
若左树深度A = 右树深度B + 1，则右树一定是满二叉树，那么右树 + 头节点 = [2^B -1] + 1，左树递归去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 请保证head为头的树，是完全二叉树
public static int nodeNum(Node head) {
    if (head == null) {
        return 0;
    }
    return bs(head, 1, mostLeftLevel(head, 1));
}

// node在第level层，h是总的深度（h永远不变，全局变量
// 以node为头的完全二叉树，节点个数是多少
public static int bs(Node node, int Level, int h) {
    //basecase，最深层，一个节点
    if (Level == h) {
        return 1;
    }
    //如果右树和左树的层数相同，左树满二叉树计算
    if (mostLeftLevel(node.right, Level + 1) == h) {
        //左树满，计算层数
        return (1 << (h - Level)) + bs(node.right, Level + 1, h);
    } else {
        //右树满，但是层数比左树小一层，所以减1
        return (1 << (h - Level - 1)) + bs(node.left, Level + 1, h);
    }
}

// 如果node在第level层，
// 求以node为头的子树，最大深度是多少
// node为头的子树，一定是完全二叉树
//Node node 以这个node节点总共有几层
//int level 这个node处于第几层，接着往下加
public static int mostLeftLevel(Node node, int level) {
    while (node != null) {
        level++;
        node = node.left;
    }
    return level - 1;
}

LRU

1
2
3
4
5
6
7
8
9
10
11
(Least Recently Used)LRU内存替换算法的实现:
假设一个HashMap最多存储3条记录，弄个时间戳，不管是get、put都更新时间戳，当要新增或者删除时，都优先移除时间戳最早的数据。

经典的只有put, get, 要求时间复杂度O(1)

使用双向链表:
越靠近尾部就是最近操作的key,越靠近头部就是最早操作的key
把一个节点拿出,或者放到最后都是O(1), 因为直接用Hash表操作

为什么不能使用单链表：
因为当要更新链表中间的节点到链表末尾时，无法找到它的parent对象指向它的next指针
1
2
3
4
5
6
7
8
9
10
11
public static class Node<K, V> {
    public K key;
    public V value;
    public Node<K, V> pre;
    public Node<K, V> next;

    public Node(K key, V value) {
        this.key = key;
        this.value = value;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
// 双向链表
// 从head到tail所有节点都是串好的
public static class NodeDoubleLinkedList<K, V> {
    private Node<K, V> head;
    private Node<K, V> tail;

    public NodeDoubleLinkedList() {
        head = null;
        tail = null;
    }

    // 如果一个新的节点加入，放到尾巴上去
    public void addNode(Node<K, V> newNode) {
        if (newNode == null) {
            return;
        }
        // newNode != null
        if (head == null) { // 双向链表中一个节点也没有
            head = newNode;
            tail = newNode;
        } else { // 双向链表中之前有节点，tail（非null）
            tail.next = newNode;
            newNode.pre = tail;
            tail = newNode;
        }
    }

    // 潜台词 ： 双向链表上一定有这个node
    // node分离出，但是node前后环境重新连接
    // node放到尾巴上去
    public void moveNodeToTail(Node<K, V> node) {
        //如果刚好是尾巴，什么都不用干
        if (this.tail == node) {
            return;
        }
        //如果刚好是头指针，不用动pre的指针
        if (this.head == node) { // 当前node是老头部
            this.head = node.next;
            this.head.pre = null;
        } else { // 当前node是中间的一个节点
            node.pre.next = node.next;
            node.next.pre = node.pre;
        }
        //把节点放到尾巴去
        node.pre = this.tail;
        node.next = null;
        this.tail.next = node;
        this.tail = node;
    }

    public Node<K, V> removeHead() {
        if (this.head == null) {
            return null;
        }
        Node<K, V> res = this.head;
        if (this.head == this.tail) { // 链表中只有一个节点的时候
            this.head = null;
            this.tail = null;
        } else {
            this.head = res.next;
            res.next = null;
            this.head.pre = null;
        }
        return res;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public static class MyCache<K, V> {
    private HashMap<K, Node<K, V>> keyNodeMap;
    private NodeDoubleLinkedList<K, V> nodeList;
    private final int capacity;
  
    //初始化时定义好LRU的空间大小
    public MyCache(int cap) {
        if (cap < 1) {
            throw new RuntimeException("should be more than 0.");
        }
        keyNodeMap = new HashMap<K, Node<K, V>>();
        nodeList = new NodeDoubleLinkedList<K, V>();
        capacity = cap;
    }

    public V get(K key) {
        if (keyNodeMap.containsKey(key)) {
            Node<K, V> res = keyNodeMap.get(key);
            nodeList.moveNodeToTail(res);
            return res.value;
        }
        return null;
    }

    public void set(K key, V value) {
        if (keyNodeMap.containsKey(key)) {
            Node<K, V> node = keyNodeMap.get(key);
            node.value = value;
            nodeList.moveNodeToTail(node);
        } else { // 这是一个新加的记录，有可能出现替换
             if (keyNodeMap.size() == capacity) {
                removeMostUnusedCache();
            }
            Node<K, V> newNode = new Node<K, V>(key, value);
            keyNodeMap.put(key, newNode);
            nodeList.addNode(newNode);
           
        }
    }

    private void removeMostUnusedCache() {
        Node<K, V> removeNode = nodeList.removeHead();
        keyNodeMap.remove(removeNode.key);
    }
}

图的遍历

1
2
3
4
5
6
7
8
9
10
给定两个字符串，记为start和to，再给定一个字符串列表list，list中一定包含to list中没有重复字符串，所有的字符串都是小写的。
规定: start每次只能改变一个字符，最终的目标是彻底变成to，但是每次变成的新字符串必须在list 中存在。
请返回所有最短的变换路径。
【举例】 
start="abc",end="cab",list={"cab","acc","cbc","ccc","cac","cbb","aab","abb"}
转换路径的方法有很多种，但所有最短的转换路径如下: 
abc -> abb -> aab -> cab
abc -> abb -> cbb -> cab
abc -> cbc -> cac -> cab
abc -> cbc -> cbb -> cab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
思路：
把List集合做成一张图，能够通过改变有一个字符变成新字符，则表示两个字符之间有边

如果有N个字符串, 每个字符串平均长度K, 怎么构建这张邻居表?
 0位置的字符串查跟1, 2, 3, ..., N-1之间有没有路径
 1位置的字符串查跟2, 3, 4, ..., N-1之间有没有路径
 2位置的字符串查跟3, 4, 5, ..., N-1之间有没有路径
复杂度: O(N^2)  两个字符串, 想知道他们之间有没有路径, 还得遍历一个O(K)才知道
生成所有邻居表复杂度: O(N^2*K)

如果字符串长度是K, 而每一个字符都是小写字母的话,这个过程是可以加速的 先把List作成hash表
把【abc】所有变化的可能性都列出来, 查每一个字符串在set里有没有,如果有就是你的邻居, 没有就忽略
可能性数量：25 * K
在hash表查的复杂度O(1): 是在每个单样本大小可以忽略的情况下，字符串在哈希表怎么查?
需要遍历你所有字符, 求出一个哈希值再去找，所以, 这里要认为复杂度是O(K)，每一个查询代价O(k)
所以这个方法的复杂度是 O(K^2) 就能找到所有邻居
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
public static List<List<String>> findMinPaths(
    String start, 
    String end,
    List<String> list) {
    list.add(start);
    //获取list中所有字符的枚举的邻居
    HashMap<String, ArrayList<String>> nexts = getNexts(list);
    
    //求所有字符串到start的最短距离是多少 宽度优先遍历
    HashMap<String, Integer> distances = getDistances(start, nexts);

    LinkedList<String> pathList = new LinkedList<>();
    List<List<String>> res = new ArrayList<>();
    getShortestPaths(start, end, nexts, distances, pathList, res);
    return res;
}

//返回words中的所有字符对应的邻居表
public static HashMap<String, ArrayList<String>> getNexts(List<String> words) {
    Set<String> dict = new HashSet<>(words); // List 所有东西放入 set
    HashMap<String, ArrayList<String>> nexts = new HashMap<>();
    for (int i = 0; i < words.size(); i++) {
        nexts.put(words.get(i), getNext(words.get(i), dict));
    }
    return nexts;
}

private static ArrayList<String> getNext(String word, Set<String> dict) {
    ArrayList<String> res = new ArrayList<String>();
    char[] chs = word.toCharArray();
    //枚举所有字符 不包括 word 和dict中的字符
    for (int i = 0; i < chs.length; i++) {
        for (char cur = 'a'; cur <= 'z'; cur++) {
            if (chs[i] != cur) {
                char tmp = chs[i];
                chs[i] = cur;
                if (dict.contains(String.valueOf(chs))) {
                    res.add(String.valueOf(chs));
                }
                chs[i] = tmp;
            }
        }
    }
    return res;
}

//图的宽度优先遍历
public static HashMap<String, Integer> getDistances(String start,
                                                    HashMap<String, ArrayList<String>> nexts) {
    HashMap<String, Integer> distances = new HashMap<>();
    distances.put(start, 0);
    Queue<String> queue = new LinkedList<String>();
    queue.add(start);
    //去重遍历过的节点
    HashSet<String> set = new HashSet<String>();
    set.add(start);
    while (!queue.isEmpty()) {
        String cur = queue.poll();
        for (String next : nexts.get(cur)) {
            if (!set.contains(next)) {
                //记录节点到start之间的层数
                distances.put(next, distances.get(cur) + 1);
                queue.add(next);
                set.add(next);
            }
        }
    }
    return distances;
}

// 现在来到了什么：cur
// 目的地：to
// 邻居表：nexts
// 最短距离表：distances
// 沿途走过的路径：path上{....}
// 答案往res里放，收集所有的最短路径
private static void getShortestPaths(
    String cur, String to,
    HashMap<String, ArrayList<String>> nexts,
    HashMap<String, Integer> distances,
    LinkedList<String> path,
    List<List<String>> res) {
    
    //路径中先添加起始点cur
    path.add(cur);
    if (to.equals(cur)) {
        //找到目标str了，生成新list添加进去
        res.add(new LinkedList<String>(path));
    } else {
        //获取起始点的邻居表
        for (String next : nexts.get(cur)) {
            //要求起始点cur到出发到next的距离是严格递增的，不能往回走，往回走则表示它肯定不是最短的
            //等同于过滤掉了较长的回环路径
            if (distances.get(next) == distances.get(cur) + 1) {
                //符合要求的邻居，递归去吧
                getShortestPaths(next, to, nexts, distances, path, res);
            }
        }
    }
    //深度优先遍历擦出轨迹，还原现场
    path.pollLast();
}

异或

1
2
一个数组的异或和是指数组中所有的数异或在一起的结果
给定一个数组arr，求最大子数组异或和。
1
2
3
4
解法一：O(N^2)
生成eor[0..i]的异或和数组 = eor[0..2] ^ eor[3..i]  
所以eor[3..i] = eor[0..2] ^ eor[0..i] ，因为 同样的数字异或之后等于0，所以eor[0..2]被消除了
通过这样求出了所有以i结尾的数组的最大异或和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static int maxXorSubarray1(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    // 准备一个前缀异或和数组eor
    // eor[i] = arr[0...i]的异或结果
    int[] eor = new int[arr.length];
    eor[0] = arr[0];
    // 生成eor数组，eor[i]代表arr[0..i]的异或和
    for (int i = 1; i < arr.length; i++) {
        eor[i] = eor[i - 1] ^ arr[i];
    }
    int max = Integer.MIN_VALUE;
    //求以j结尾的异或和数组的最大值
    for (int j = 0; j < arr.length; j++) {
        // 依次尝试arr[0..j]、arr[1..j]..arr[i..j]..arr[j..j]
        //求 eor[i,j] = eor[0,j] ^ eor[0,i-1]
        for (int i = 0; i <= j; i++) { 
            max = Math.max(max, i == 0 ? eor[j] : eor[j] ^ eor[i - 1]);
        }
    }
    return max;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
解法二：O(N)
假设eor[0..i]的异或和 = 0110，由于异或和的不确定性，所以无法很快筛选出以i结尾时，它的最大异或和是什么?
将eor[0..i-1]的结果都添加到前缀树中，根据前缀树筛选出一个和eor[0..i]异或之后，最大的值
前缀树中默认需要添加0000的前缀分支

假设eor[0..1] = 1010 eor[0..2] = 0101 eor[0..i] = 0110
【0110】根据前缀树中，挑选出它最期望遇到的能让他变得更大的值，照顾高位先变1
在不考虑符号位的情况下，它希望第一位是1,第二位和第三位是0，第四位是1，才能达到1111的最大值
所以前缀树优先找第一位是【1】，第二、三位是【0】的异或和
由于前缀树中没有[1001]开头的路径，所以选择最匹配的则是[1010]，这个[1010]对应的是eor[0..1]

那么以i位置的最大异或和肯定是 eor[0..i] ^ eor[0..1] = eor[2..i]

在考虑符号位的情况下，若最高位是0，它最期望遇到的最高位也是0
若有负数，则同理，最高位期待和自己相同的符号位
若最高位符号位是1，也是优先照顾高位先变成1，因为负数是 整数 取反码 加一

所以最终的贪心策略：
1.期望遇到相同的符号位
2.优先让高位（非符号位）变成1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int maxXorSubarray2(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int max = Integer.MIN_VALUE;
    int eor = 0; // 0..i 异或和
    // 前缀树 -> numTrie
    NumTrie numTrie = new NumTrie();
    numTrie.add(0); // 一个数也没有的时候，异或和是0
    for (int i = 0; i < arr.length; i++) {
        eor ^= arr[i]; // eor -> 0..i异或和
        // X, 0~0 , 0~1, .., 0~i-1
        max = Math.max(max, numTrie.maxXor(eor));
        numTrie.add(eor);
    }
    return max;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 前缀树的节点类型，每个节点向下只可能有走向0或1的路
// node.nexts[0] == null 0方向没路
// node.nexts[0] != null 0方向有路
public static class Node {
    public Node[] nexts = new Node[2];
}

// 基于本题，定制前缀树的实现
public static class NumTrie {
    // 头节点
    public Node head = new Node();

    // 把某个数字newNum加入到这棵前缀树里
    // num是一个32位的整数，所以加入的过程一共走32步
    public void add(int newNum) {
        Node cur = head;
        for (int move = 31; move >= 0; move--) {
            // 从高位到低位，取出每一位的状态，如果当前状态是0，
            // path(int) = 0
            // ，如果当前状态是1
            // path(int) = 1
            int path = ((newNum >> move) & 1);
            // 无路新建、有路复用
            cur.nexts[path] = cur.nexts[path] == null ? new Node() : cur.nexts[path];
            cur = cur.nexts[path];
        }
    }

    // 该结构之前收集了一票数字，并且建好了前缀树
    // sum,和 谁 ^ 最大的结果（把结果返回）
    public int maxXor(int sum) {
        Node cur = head;
        int res = 0;
        for (int move = 31; move >= 0; move--) {
            //move位置上是1还是0
            int path = (sum >> move) & 1;
            // 期待的路
            //若move == 31，则表示符号位，我期待和path相同的值
            //若不是，则我期待和他相反的值，因为 0 ^ 1 = 1
            int best = move == 31 ? path : (path ^ 1);
            
            // 前缀树中实际走的路,
            best = cur.nexts[best] != null ? best : (best ^ 1);
            
            // (path ^ best) 当前位位异或完的结果，赋值到res的第move位中
            res |= (path ^ best) << move;
            cur = cur.nexts[best];
        }
        return res;
    }
}
1
给定一个数组arr，哪一种划分下一个数组异或和为零的部分最多，返回最多能划分出几块异或和为零的部分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
思路：假设答案法
一个数组arr:
0~0范围上最多能划分出几个异或和子数组
0~1范围上最多能划分出几个异或和子数组
0~2范围上最多能划分出几个异或和子数组
...
0~N-1范围上最多能划分出几个异或和子数组

假设0..i上的一种切法, 假设这种切法下, 异或和为零的子数组部分最多
按照结尾来划分可能性
i位置的数一定是最后一个部分的最后一个数

可能性一：
i位置的数所在最后一个部分不是异或和为零  -> dp[0..i] = dp[0..i - 1]

可能性二：
i位置的数所在最后一个部分是异或和为零
假设以j开头, [j..i] 中间 不可能存在一个k, 让k...i异或和为零,j一定是i的左边离i最近的一个开头
那么dp[0..i] = dp[0..j] + 1

如果0~i的整体异或和是 1000, 怎么找这个j?
计算某个区间[0..i]上,最晚出现异或和 = 1000 的位置k，那么 j = k + 1， eor[j..i] = 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static int mostEOR(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int N = arr.length;
    int[] dp = new int[N]; // dp[i] = 0
    //用来缓存每个异或和的结果对应出现的最晚位置
    HashMap<Integer, Integer> map = new HashMap<>();
  
    //最左边的边界值，整体异或和 = 0时的判断
    map.put(0, -1);
    int sum = 0;
    for (int i = 0; i < arr.length; i++) {
        sum ^= arr[i];
        if (map.containsKey(sum)) {
            int pre = map.get(sum);
            //若整体异或和=0，且边界在最左边，则dp[i]=1
            dp[i] = pre == -1 ? 1 : (dp[pre] + 1);
        }
        if (i > 0) {
            dp[i] = Math.max(dp[i - 1], dp[i]);
        }
        //存储最晚出现异或和的位置，若出现0，会把最左边-1的边界给更新
        map.put(sum, i);
    }
    return dp[dp.length - 1];
}
1
2
3
4
5
6
给定一个只由 0(假)、1(真)、&(逻辑与)、|(逻辑或)和^(异或)五种字符组成 的字符串express
再给定一个布尔值 desired。返回express能有多少种组合 方式，可以达到desired的结果。
【举例】
express="1^0|0|1"，desired=false
只有 1^((0|0)|1)和 1^(0|(0|1))的组合可以得到 false，返回 2。 express="1"，desired=false
无组合则可以得到false，返回0
1
2
3
4
5
6
7
8
9
10
11
12
13
思路：假设答案法
根据题意：
偶数位置必须是数字，奇数位置必须是运算符号，长度必须为奇数

分解：假设每一个符号都是最后结合
假设必须以i位置的& 做最后一步二元结合的符号的情况下, 答案是几种?
1.期望True:
  [L..i-1]是T，结果A种，[i+1..R]是T，结果B种 数量：A*B种
2.期望False:
  [L..i-1]是T，结果A种，[L..i-1]是F，结果B种
  [i+1..R]是T，结果C种，[i+1..R]是F，结果D种
  数量： A*D + B*C + B*D
【|】和【^】符号同理推算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
//暴力递归
public static int num1(String express, boolean desired) {
    if (express == null || express.equals("")) {
        return 0;
    }
    char[] exp = express.toCharArray();
    if (!isValid(exp)) {
        return 0;
    }
    return f(exp, desired, 0, exp.length - 1);
}

// exp[L..R] 返回期待为desired的方法数
// 潜台词：L R 必须是偶数位置
public static int f(char[] exp, boolean desired, int L, int R) {
    if (L == R) { // base case 1
        if (exp[L] == '1') {
            return desired ? 1 : 0;
        } else { // '0'
            return desired ? 0 : 1;
        }
    }

    // L..R
    int res = 0;
    if (desired) { // 期待为true
        // i位置尝试L..R范围上的每一个逻辑符号，都是最后结合的
        for (int i = L + 1; i < R; i += 2) {
            // exp[i] 一定压中逻辑符号
            switch (exp[i]) {
                case '&':
                    res += f(exp, true, L, i - 1) * f(exp, true, i + 1, R);
                    break;
                case '|':
                    res += f(exp, true, L, i - 1) * f(exp, false, i + 1, R);
                    res += f(exp, false, L, i - 1) * f(exp, true, i + 1, R);
                    res += f(exp, true, L, i - 1) * f(exp, true, i + 1, R);
                    break;
                case '^':
                    res += f(exp, true, L, i - 1) * f(exp, false, i + 1, R);
                    res += f(exp, false, L, i - 1) * f(exp, true, i + 1, R);
                    break;
            }
        }
    } else { // 期待为false
        for (int i = L + 1; i < R; i += 2) {
            switch (exp[i]) {
                case '&':
                    res += f(exp, false, L, i - 1) * f(exp, true, i + 1, R);
                    res += f(exp, true, L, i - 1) * f(exp, false, i + 1, R);
                    res += f(exp, false, L, i - 1) * f(exp, false, i + 1, R);
                    break;
                case '|':
                    res += f(exp, false, L, i - 1) * f(exp, false, i + 1, R);
                    break;
                case '^':
                    res += f(exp, true, L, i - 1) * f(exp, true, i + 1, R);
                    res += f(exp, false, L, i - 1) * f(exp, false, i + 1, R);
                    break;
            }
        }
    }
    return res;
}

//校验是否有效字符串，判断奇数是否是符号位，偶数是否是数字，长度是否是奇数
public static boolean isValid(char[] exp) {
    if ((exp.length & 1) == 0) {
        return false;
    }
    for (int i = 0; i < exp.length; i = i + 2) {
        if ((exp[i] != '1') && (exp[i] != '0')) {
            return false;
        }
    }
    for (int i = 1; i < exp.length; i = i + 2) {
        if ((exp[i] != '&') && (exp[i] != '|') && (exp[i] != '^')) {
            return false;
        }
    }
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//动态规划
public static int dpLive(String express, boolean desired) {
    char[] str = express.toCharArray();
    int N = str.length;
    int[][] tMap = new int[N][N];
    int[][] fMap = new int[N][N];
    for (int i = 0; i < N; i += 2) {
        tMap[i][i] = str[i] == '1' ? 1 : 0;
        fMap[i][i] = str[i] == '0' ? 1 : 0;
    }
    for (int row = N - 3; row >= 0; row -= 2) {
        for (int col = row + 2; col < N; col += 2) {
            // row..col tMap fMap
            for (int i = row + 1; i < col; i += 2) {
                switch (str[i]) {
                    case '&':
                        tMap[row][col] += tMap[row][i - 1] * tMap[i + 1][col];
                        break;
                    case '|':
                        tMap[row][col] += tMap[row][i - 1] * fMap[i + 1][col];
                        tMap[row][col] += fMap[row][i - 1] * tMap[i + 1][col];
                        tMap[row][col] += tMap[row][i - 1] * tMap[i + 1][col];
                        break;
                    case '^':
                        tMap[row][col] += tMap[row][i - 1] * fMap[i + 1][col];
                        tMap[row][col] += fMap[row][i - 1] * tMap[i + 1][col];
                        break;
                }
                switch (str[i]) {
                    case '&':
                        fMap[row][col] += fMap[row][i - 1] * tMap[i + 1][col];
                        fMap[row][col] += tMap[row][i - 1] * fMap[i + 1][col];
                        fMap[row][col] += fMap[row][i - 1] * fMap[i + 1][col];
                        break;
                    case '|':
                        fMap[row][col] += fMap[row][i - 1] * fMap[i + 1][col];
                        break;
                    case '^':
                        fMap[row][col] += tMap[row][i - 1] * tMap[i + 1][col];
                        fMap[row][col] += fMap[row][i - 1] * fMap[i + 1][col];
                        break;
                }	
            }
        }
    }
    return desired ? tMap[0][N-1]  : fMap[0][N-1];	
}
1
2
3
给出一组正整数arr，你从第0个数向最后一个数，
每个数的值表示你从这个位置可以向右跳跃的最大长度
计算如何以最少的跳跃次数跳到最后一个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//动态规划 从左往右模型
public static int jump(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int step = 0; // 跳了多少步
    int cur = 0; // step步内，最右的边界
    int next = 0;// step+1步内，最右的边界
    for (int i = 0; i < arr.length; i++) {
        //如果当前i超过了cur的边界，则增加一步，并且把下一步的边界赋值到cur上
        if (cur < i) {
            step++;
            cur = next;
        }
        //step步内能到达的点，它下一跳，能跳到多远：i + arr[i]
        next = Math.max(next, i + arr[i]);
    }
    return step;
}
1
一个字符串至少切几刀,能让切出来的部分全是回文串
1
2
3
4
5
6
7
8
9
思路:
[0..0]..[0..1]...[0..N-1]
[1..1]..[1..2]...[1..N-1]
以每个i做切割,时间复杂度O(N^2),再加上需要再遍历一遍判断区间内的字符串是否是回文O(N)
所以总复杂度O(N^3)

可以通过先做dp表，标记所有[L..R]上的字符是否是回文，阶数减一阶
是回文的条件：arr[L] == arr[R] && [L+1][R-1]是回文(查dp表)
dp表优先填写对角线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static int minParts(String s) {
    if (s == null || s.length() == 0) {
        return 0;
    }
    if (s.length() == 1) {
        return 1;
    }
    char[] str = s.toCharArray();
    int N = str.length;
    boolean[][] isP = new boolean[N][N];
    //一个字符，必定回文
    for (int i = 0; i < N; i++) {
        isP[i][i] = true;
    }
    //填写第二条对角线，L和R都是一个字符
    for (int i = 0; i < N - 1; i++) {
        isP[i][i + 1] = str[i] == str[i + 1];
    }
    //从第三条对小件开始填起
    for (int row = N - 3; row >= 0; row--) {
        for (int col = row + 2; col < N; col++) {
            isP[row][col] = str[row] == str[col] && isP[row + 1][col - 1];
        }
    }
    int[] dp = new int[N + 1];
    for (int i = 0; i <= N; i++) {
        dp[i] = Integer.MAX_VALUE;
    }
    //end..N-1需要用到N的值，补个长度0
    dp[N] = 0;
    for (int i = N - 1; i >= 0; i--) {
        for (int end = i; end < N; end++) {
            // i..end
            if (isP[i][end]) {
                //若是回文，他的回文等于end + 1的回文数 + 1
                dp[i] = Math.min(dp[i], 1 + dp[end + 1]);
            }
        }
    }
    return dp[0];
}
1
2
3
4
5
给定两个有序数组arr1和arr2，再给定一个正数K

求两个数累加和最大的前K个，两个数必须分别来自arr1和arr2
如arr1={3,5,7,9} arr2={2,4,8,10} K = 3
结果:{9+10,9+8,7+8}
1
2
3
4
5
6
7
8
9
思路：
arr1和arr2建立一张二维表，用来存储arr1和arr2对应下标数值的和
那么右下角[N-1][M-1]=arr1[N-1] + arr2[M-1]必然是最大的，因为有序
然后准备个大根堆，将右下角的点先写入大根堆中
然后依次弹出大根堆的堆顶做答案，并写入该点左边和上边的两个点
假设大根堆弹出的点位置是[i][j]，将[i-1][j]和[i][j-1]放入大根堆中

需要注意：要保证同一个点的数据不能重复进入大根堆中
时间复杂度O(N * logK)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 放入大根堆中的结构
public static class Node {
    public int index1;// arr1中的位置
    public int index2;// arr2中的位置
    public int sum;// arr1[index1] + arr2[index2]的值

    public Node(int i1, int i2, int s) {
        index1 = i1;
        index2 = i2;
        sum = s;
    }
}

// 生成大根堆的比较器
public static class MaxHeapComp implements Comparator<Node> {
    @Override
    public int compare(Node o1, Node o2) {
        return o2.sum - o1.sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public static int[] topKSum(int[] arr1, int[] arr2, int topK) {
    if (arr1 == null || arr2 == null || topK < 1) {
        return null;
    }
    // topK过滤，最多只能提供N * M 个
    topK = Math.min(topK, arr1.length * arr2.length);

    int[] res = new int[topK];
    int resIndex = 0;

    PriorityQueue<Node> maxHeap = new PriorityQueue<>(new MaxHeapComp());

    // set[i][j] == false, arr1[i]  arr2[j] 之前，没进过
    // set[i][j] == true;  arr1[i]  arr2[j] 之前，进过
    boolean[][] set = new boolean[arr1.length][arr2.length];
    int i1 = arr1.length - 1;
    int i2 = arr2.length - 1;
    maxHeap.add(new Node(i1, i2, arr1[i1] + arr2[i2]));
    set[i1][i2] = true;
    while (resIndex != topK) {
        Node curNode = maxHeap.poll();
        //收集答案
        res[resIndex++] = curNode.sum;
        i1 = curNode.index1;
        i2 = curNode.index2;
        if (i1 - 1 >= 0 && !set[i1 - 1][i2]) {
            set[i1 - 1][i2] = true;
            maxHeap.add(new Node(i1 - 1, i2, arr1[i1 - 1] + arr2[i2]));
        }
        if (i2 - 1 >= 0 && !set[i1][i2 - 1]) {
            set[i1][i2 - 1] = true;
            maxHeap.add(new Node(i1, i2 - 1, arr1[i1] + arr2[i2 - 1]));
        }
    }
    return res;
}
1
2
3
4
5
给定一个正数数组arr，返回该数组能不能分成4个部分，并且每个部分的累加和相等，切分位置的数不要。
例如:
arr=[3, 2, 4, 1, 4, 9, 5, 10, 1, 2, 2] 返回true
三个切割点下标为2, 5, 7. 切出的四个子数组为[3,2], [1,4], [5], [1,2,2]，
累加和都是5
1
2
3
4
5
6
7
8
思路：
根据题意，arr.length > 7，且第一个切割点 1 < i < length - 6，否则无法满足
先建立hash表,Key是0..i的累加和sum，Value是对应的index
i = 1 开始枚举每个下标做切割点
尝试hash.get(sum[0..i-1]) = V的情况下，是否存在第二个切割点：j = hash.get(sum[2V + arr[i]])
以此类推，第三个切割点k = 3V + arr[i] + arr[j]...

时间复杂度：O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static boolean canSplits2(int[] arr) {
    if (arr == null || arr.length < 7) {
        return false;
    }
    // key 某一个累加和， value出现的位置
    HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
    int sum = arr[0];
    for (int i = 1; i < arr.length; i++) {
        map.put(sum, i);
        sum += arr[i];
    }
    int lsum = arr[0]; // 第一刀左侧的累加和
    for (int s1 = 1; s1 < arr.length - 5; s1++) { // s1是第一刀的位置
        int checkSum = lsum * 2 + arr[s1]; // 100 x 100   100*2 + x
        if (map.containsKey(checkSum)) {
            int s2 = map.get(checkSum); // j -> y
            checkSum += lsum + arr[s2];
            if (map.containsKey(checkSum)) { // 100 * 3 + x + y
                int s3 = map.get(checkSum); // k -> z
                if (checkSum + arr[s3] + lsum == sum) {
                    return true;
                }
            }
        }
        lsum += arr[s1];
    }
    return false;
}
1
2
3
4
5
6
给定三个字符串str1、str2和aim，如果aim包含且仅包含来自str1和str2的所有字符
而且在aim中属于str1的字符之间保持原来在str1中的顺序，
属于str2的字符之间保持原来在str2中的顺序
那么称aim是str1和str2的交错组成。实现一个函数，判断aim是 否是str1和str2交错组成
【举例】 str1="AB"，str2="12"。
那么"AB12"、"A1B2"、"A12B"、"1A2B"和"1AB2"等都是 str1 和 str2 的 交错组成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
思路：
动态规划二维表dp[N+1][M+1]，value存储布尔值
dp[i][j]含义：
  str1拿出前缀i长度, 对应下标 [0..i-1] 
  str2拿出前缀j长度, 对应下标 [0..j-1]
  能否交错组成str3的前缀[i+j]长度

先填第一行第一列：拿str1和str2去和str3做比较，前缀相等则True，若出现一个Flase，后面全是False
然后一行一行得填写，最后取出答案dp[N][M]

可能性：
1.str3[i+j-1] == str1[i] && dp[i][j] = dp[i-1][j] -->True
2.str3[i+j-1] == str1[j] && dp[i][j] = dp[i][j-1] -->True
3.否则False

该题的动态规划依赖了[i,j]的左边的值和上边的值，可以进行动态规划空间压缩技巧，使用一个一维数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static boolean isCross1(String s1, String s2, String ai) {
    if (s1 == null || s2 == null || ai == null) {
        return false;
    }
    char[] str1 = s1.toCharArray();
    char[] str2 = s2.toCharArray();
    char[] aim = ai.toCharArray();
    //长度不等直接返回false
    if (aim.length != str1.length + str2.length) {
        return false;
    }
    boolean[][] dp = new boolean[str1.length + 1][str2.length + 1];
    dp[0][0] = true;
    //填写第一列
    for (int i = 1; i <= str1.length; i++) {
        if (str1[i - 1] != aim[i - 1]) {
            break;
        }
        dp[i][0] = true;
    }
    //填写第一行
    for (int j = 1; j <= str2.length; j++) {
        if (str2[j - 1] != aim[j - 1]) {
            break;
        }
        dp[0][j] = true;
    }
    //dp规划
    for (int i = 1; i <= str1.length; i++) {
        for (int j = 1; j <= str2.length; j++) {
            if (	
                (str1[i - 1] == aim[i + j - 1] && dp[i - 1][j])
                || 
                (str2[j - 1] == aim[i + j - 1] && dp[i][j - 1])	
            ) {
                dp[i][j] = true;					
            }
        }
    }
    return dp[str1.length][str2.length];
}
1
2
3
给定一个无序数组arr，如果只能再一个子数组上排序

返回如果让arr整体有序，需要排序的最短子数组长度
1
2
3
4
5
6
思路：
从左往右遍历，记录更新i左边的最大值。若i < max，记录最靠近右边 < max 的i位置 -> 确定了[i+1..N]无需调整
从右往左遍历，记录更新j右边的最小值。若j > max，记录最靠近坐边 > max 的j位置 -> 确定了[0..j-1]无需调整
区间[j,i]就是需要排序的数组

时间复杂度O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static int getMinLength(int[] arr) {
    if (arr == null || arr.length < 2) {
        return 0;
    }
    int min = arr[arr.length - 1];
    int noMinIndex = -1;
    for (int i = arr.length - 2; i != -1; i--) {
        if (arr[i] > min) {
            noMinIndex = i;
        } else {
            min = Math.min(min, arr[i]);
        }
    }
    if (noMinIndex == -1) {
        return 0;
    }
    int max = arr[0];
    int noMaxIndex = -1;
    for (int i = 1; i != arr.length; i++) {
        if (arr[i] < max) {
            noMaxIndex = i;
        } else {
            max = Math.max(max, arr[i]);
        }
    }
    return noMaxIndex - noMinIndex + 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
给定一个正数数组 arr，其中所有的值都为整数，以下是最小不可组成和的概念:
把 arr 每个子集内的所有元素加起来会出现很多值，其中最小的记为 min，最大的记为max 在区间[min,max]上
如果有数不可以被arr某一个子集相加得到，那么其中最小的那个数是arr 的最小不可组成和 在区间[min,max]上
如果所有的数都可以被arr的某一个子集相加得到，那么max+1是arr的最 小不可组成和
请写函数返回正数数组 arr 的最小不可组成和。

【举例】
arr=[3,2,5]。子集{2}相加产生 2 为 min，子集{3,2,5}相加产生 10 为 max。
在区间[2,10] 上，4、 6 和 9 不能被任何子集相加得到，其中 4 是 arr 的最小不可组成和。 
arr=[1,2,4]。子集{1}相加产生 1 为 min，子集{1,2,4}相加产生 7 为 max。
在区间[1,7]上， 任何 数都可以被子集相加得到，所以 8 是 arr 的最小不可组成和。

【进阶】
如果已知正数数组 arr 中肯定有 1 这个数，是否能更快地得到最小不可组成和?
1
2
3
4
5
6
7
8
9
10
11
问题一：
经典的背包问题
arr数组的index做样本的行，sum[0..N-1]做样本的列，dp[i][j]=True/False
等同于背包问题的w[]做行，bag做列
最后结果 = dp[N-1][0..sum]中为False的数据

进阶：
先让arr有序，1一定是落在第一个位置，定义一个range变量
若arr[i] <= range + 1 ，则 range += arr[i] 表示从[min...range]范围内都能够通过累加得到
若arr[i] > range + 1，表示往后的arr[i]肯定都是更大的，所以最小不可组成和 = range + 1
若遍历完集合都达标，则最小不可组成和 = range + 1，因为此时的range达到了所有数组的累加和大小max
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 已知arr中肯定有1这个数
public static int unformedSum3(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    Arrays.sort(arr); // O (N * logN)
    int range = 1;
    for (int i = 1; i != arr.length; i++) {
        if (arr[i] > range + 1) {
            return range + 1;
        } else {
            range += arr[i];
        }
    }
    return range + 1;
}
1
2
3
4
5
6
给定一个有序的正数数组arr和一个正数aim，如果可以自由选择arr中的数字，想累加得 到 1~aim 范围上所有的数，返回arr最少还缺几个数。
【举例】
arr = {1,2,3,7}， aim = 15
想累加得到 1~15 范围上所有的数，arr 还缺 14 这个数，所以返回1 
arr = {1,5,7}， aim = 15
想累加得到 1~15 范围上所有的数，arr 还缺 2 和 4，所以返回2
1
2
3
4
思路：
借用上题的思路，arr[i] > range时，缺啥补啥，比如补range + 1的值，然后range += range + 1
再次比较arr[i]..周而复始
若arr遍历完了，range还没达到aim，接着扩补数字接着扩
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// arr请保证有序，且正数
public static int minPatches(int[] arr, int aim) {
    int patches = 0; // 缺多少个数字
    long range = 0; // 已经完成了1 ~ range的目标
    for (int i = 0; i != arr.length; i++) {
        // 1~range
        // 1 ~ arr[i]-1
        while (arr[i] > range + 1) { // arr[i] 1 ~ arr[i]-1
            range += range + 1; // range + 1 是缺的数字
            patches++;
            if (range >= aim) {
                return patches;
            }
        }
        range += arr[i];
        if (range >= aim) {
            return patches;
        }
    }
    while (aim >= range + 1) {
        range += range + 1;
        patches++;
    }
    return patches;
}
1
2
3
4
5
6
在一个字符串中找到没有重复字符子串中最长的长度。
例如:
abcabcbb没有重复字符的最长子串是abc，长度为3 
bbbbb，答案是b，长度为1
pwwkew，答案是wke，长度是3
要求:答案必须是子串，"pwke" 是一个子字符序列但不是一个子字符串。
1
2
3
4
5
思路：
遇到子串、子序列，优先想到的是以i开头....以i结尾...的dp表
建个map缓存 arr[i]上一次出现的位置
dp[i]表示以i结尾，最长无重复字符子串的长度
dp[i] = Math.min(arr[i]上一次出现的位置, i - dp[i-1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int maxUnique(String str) {
    if (str == null || str.equals("")) {
        return 0;
    }
    Map<Character, Integer> indexMap = new HashMap<>();
    char[] chars = str.toCharArray();
    int max = 0;
    int pre = -1;
    for (int i = 0; i < chars.length; i++) {
        pre = Math.max(indexMap.getOrDefault(chars[i], -1), pre);
        max = Math.max(max, i - pre);
        indexMap.put(chars[i], i);
    }
    return max;
}
1
2
3
一个数组中，如果两个数的公共因子有大于1的，则认为这两个数之间有通路
返回数组中，有多少个独立的域
如：[10,5,7,4]， 有两个独立的域
1
2
3
4
5
6
7
8
9
10
11
12
13
14
思路：
解法一：
每个数都是并查集的集合，判断每个数下标开始到数组结束，两两是否有公共因子，有则合并，时间复杂度O(N^2)

解法二：
假设arr里的数值范围不是很大，算出每个数的[质数因子,index]，相同的质数因子通过并查集合并。
假设一个数V，判断一个数是否是质数，时间复杂度O(V)，得到V的质数因子O(根号V)，所以整体复杂度O(N * V)

所以解法一和解法二的权衡在于N和V哪个大

解法三：
将一个数拆成多对，比如100，根号100 = 10，从1开始试到10就停。
[2,50]、[4,25]、[5,20]、[10、10]，并查集中有相同因子，则合并。
获得键值对的代价是O(根号V)，所以总代价是O(N * 根号V)
1
2
3
4
//求两个数的最大公约数，辗转相除法，背！
public static int gcd(int m, int n) {
    return n == 0 ? m : gcd(n, m % n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
//解法一：
// arr中没有小于1的数
public static int largestComponentSize(int[] arr) {
    UnionFindSet1 set = new UnionFindSet1(arr.length);
    for (int i = 0; i < arr.length; i++) {
        for (int j = i + 1; j < arr.length; j++) {
            if (gcd(arr[i], arr[j]) != 1) {
                set.union(i, j);
            }
        }
    }
    return set.maxSize();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//解法三
public static int largestComponentSize2(int[] arr) {
    UnionFindSet2 unionFind = new UnionFindSet2(arr.length);
    // key 是某一个因子，
    // value 是包含key因子的，其中一个数的位置
    HashMap<Integer, Integer> fatorsMap = new HashMap<>();
    for (int i = 0; i < arr.length; i++) {
        int num = arr[i];
        int limit = (int) Math.sqrt(num); // 1 ~ 根号num
        for (int j = 1; j <= limit; j++) { // j是现在试的因子
            if (num % j == 0) { // num含有j的因子
                if (j != 1) { // 这个因子不是1
                    // j
                    if (!fatorsMap.containsKey(j)) { // 当前数是含有j因子的第一个数
                        fatorsMap.put(j, i);
                    } else {
                        unionFind.union(fatorsMap.get(j), i);
                    }
                }
                int other = num / j; // other * j == num
                if (other != 1) { // num含有other的因子
                    if (!fatorsMap.containsKey(other)) {
                        fatorsMap.put(other, i);
                    } else {
                        unionFind.union(fatorsMap.get(other), i);
                    }
                }
            }
        }
    }
    return unionFind.maxSize();
}
1
2
3
4
给定一个全是小写字母的字符串str，删除多余字符，使得每种字符只保留一个，并让 最终结果字符串的字典序最小
【举例】
str = "acbc"，删掉第一个'c'，得到"abc"，是所有结果字符串中字典序最小的。
str = "dbcacbca"，删掉第一个'b'、第一个'c'、第二个'c'、第二个'a'，得到"dabc"， 是所有结 果字符串中字典序最小的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
贪心思路：
统计词频，然后从左往右依次遍历字符，遍历到的词，词频--
假设遍历到i位置时，某个字母词频为0，这时候停下来，第一个字符在[0..i]位置上挑
挑[0,i]位置上，字典序最小，且index最小的字母，假设字母 = 'a',index = k
那么大于k的位置的'a'全部删掉，在[k+1,N-1]的范围上接着周二复始跳第二个字母

例子：
str = "daccbdbaccdbba"
次数统计：
a : 3	b : 4	c : 4	d : 3
遍历到"daccbdbacc" 时停，因为这时候后面 'c' 词频 = 0，在里面中挑出 最小字母'a'，index = 1
重新计算 str = “ccbdbccdbb” 周而复始，挑第二个字母

假设有K种字符，str长度是N，要挑K次，所以时间复杂度O(N * K)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 在str中，每种字符都要保留一个，让最后的结果，字典序最小 ，并返回
public static String remove(String str) {
    if(str == null || str.length() < 2) {
        return str;
    }
    int[] map = new int[256];
    //统计词频
    for(int  i = 0;i< str.length();i++) {
        map[str.charAt(i)]++;
    }
    int minACSIndex = 0;
    for(int i = 0 ; i < str.length();i++) {
        //减少到0 break
        if(--map[str.charAt(i)] == 0) {
            break;
        }else {
            //顺便计算最小的字母是什么，若重复，存储的是第一个index
            minACSIndex = str.charAt(minACSIndex) > str.charAt(i) ? i : minACSIndex;
        }
    }
    return String.valueOf(str.charAt(minACSIndex)) + 
        remove (   
        str
        .substring(minACSIndex+1)
        .replaceAll(String.valueOf(str.charAt(minACSIndex)), "")   
    )
        ;
}
1
给定两个数组arrx和arry，长度都为N。代表二维平面上有N个点，第i个点的x 坐标和y坐标分别为arrx[i]和arry[i]，返回求一条直线最多能穿过多少个点?
1
2
3
4
5
6
7
思路：
以每个点(x,y)为必须经过的点，计算：
1.和(x,y)重合的点数量
2.相同 x坐标的点的数量
3.相同 y坐标的点的数量
4.相同斜率的点的数量
这个点经过的最多的点 = Max(2,3,4)情况 + 1情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public static int maxPoints(Point[] points) {
    if (points == null) {
        return 0;
    }
    if (points.length <= 2) {
        return points.length;
    }
    //key：分子  value：分母表  表示斜率
    Map<Integer, Map<Integer, Integer>> map = new HashMap<Integer, Map<Integer, Integer>>();
    int result = 0;
    for (int i = 0; i < points.length; i++) {
        map.clear();
        int samePosition = 1;
        int sameX = 0;
        int sameY = 0;
        int line = 0;
        for (int j = i + 1; j < points.length; j++) {
            int x = points[j].x - points[i].x;
            int y = points[j].y - points[i].y;
            if (x == 0 && y == 0) {
                samePosition++;
            } else if (x == 0) {
                sameX++;
            } else if (y == 0) {
                sameY++;
            } else {
                int gcd = gcd(x, y);
                x /= gcd;
                y /= gcd;
                if (!map.containsKey(x)) {
                    map.put(x, new HashMap<Integer, Integer>());
                }
                if (!map.get(x).containsKey(y)) {
                    map.get(x).put(y, 0);
                }
                map.get(x).put(y, map.get(x).get(y) + 1);
                line = Math.max(line, map.get(x).get(y));
            }
        }
        result = Math.max(result, Math.max(Math.max(sameX, sameY), line) + samePosition);
    }
    return result;
}

// 保证初始调用的时候，a和b不等于0
public static int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}
1
2
3
4
5
int[] d，d[i]：i号怪兽的能力
int[] p，p[i]：i号怪兽要求的钱
开始时你的能力是0，你的目标是从0号怪兽开始，通过所有的怪兽。
如果你当前的能力，小于i号怪兽的能力，你必须付出p[i]的钱，贿赂这个怪兽，然后怪兽就会加入你，他的能力直接累加到你的能力上；如果你当前的能力，大于等于i号怪兽的能力，你可以选择直接通过，你的能力并不会下降，你也可以选择贿赂这个怪兽，然后怪兽就会加入你，他的能力直接累加到你的能力上。
返回通过所有的怪兽，需要花的最小钱数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// int[] d d[i]：i号怪兽的武力
// int[] p p[i]：i号怪兽要求的钱
// hp 当前你所具有的能力
// index 来到了第index个怪兽的面前

// 目前，你的能力是hp，你来到了index号怪兽的面前，如果要通过后续所有的怪兽，
// 请返回需要花的最少钱数
//暴力递归
public static long process(int[] d, int[] p, int hp, int index) {
    if (index == d.length) {
        return 0;
    }
    if (hp < d[index]) {
        return p[index] + process(d, p, hp + d[index], index + 1);
    } else { // 可以贿赂，也可以不贿赂
        return Math.min(p[index] + process(d, p, hp + d[index], index + 1), process(d, p, hp, index + 1));
    }
}

public static long func1(int[] d, int[] p) {
    return process(d, p, 0, 0);
}
1
2
3
4
5
6
7
上面解法暴力递归能改动态规划，以index为行，hp为列的二维数组，value存储花费的钱数，但是如果hp很大，这个dp表会很大
可以用花费的钱数当列，dp[i][j] 表示[0..i]范围上，花了j块钱，当前的最大能力值

可能性一：
dp[i-1][j]能力大于i号怪兽，可以不花钱 也就是 dp[i-1][j] > d[i]  --> dp[i][j] = dp[i-1][j]
可能性二：
dp[i][j]，也就是严格花j块钱，当前i的怪兽需要花k块钱，那么，dp[i][j] = d[i] + dp[i-1][j-k]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public static long func3(int[] d, int[] p) {
    int sum = 0;
    for (int num : p) {
        sum += num;
    }
    // dp[i][j]含义：
    // 能经过0～i的怪兽，且花钱为j（花钱的严格等于j）时的武力值最大是多少？
    // 如果dp[i][j]==-1，表示经过0～i的怪兽，花钱为j是无法通过的，或者之前的钱怎么组合也得不到正好为j的钱数
    int[][] dp = new int[d.length][sum + 1];
    for (int i = 0; i < dp.length; i++) {
        for (int j = 0; j <= sum; j++) {
            dp[i][j] = -1;
        }
    }
    // 经过0～i的怪兽，花钱数一定为p[0]，达到武力值d[0]的地步。其他第0行的状态一律是无效的
    dp[0][p[0]] = d[0];
    for (int i = 1; i < d.length; i++) {
        for (int j = 0; j <= sum; j++) {
            // 可能性一，为当前怪兽花钱
            // 存在条件：
            // j - p[i]要不越界，并且在钱数为j - p[i]时，要能通过0～i-1的怪兽，并且钱数组合是有效的。
            if (j >= p[i] && dp[i - 1][j - p[i]] != -1) {
                dp[i][j] = dp[i - 1][j - p[i]] + d[i];
            }
            // 可能性二，不为当前怪兽花钱
            // 存在条件：
            // 0~i-1怪兽在花钱为j的情况下，能保证通过当前i位置的怪兽
            if (dp[i - 1][j] >= d[i]) {
                // 两种可能性中，选武力值最大的
                dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
            }
        }
    }
    int ans = 0;
    // dp表最后一行上，dp[N-1][j]代表：
    // 能经过0～N-1的怪兽，且花钱为j（花钱的严格等于j）时的武力值最大是多少？
    // 那么最后一行上，最左侧的不为-1的列数(j)，就是答案
    for (int j = 0; j <= sum; j++) {
        if (dp[d.length - 1][j] != -1) {
            ans = j;
            break;
        }
    }
    return ans;
}
1
给定一个字符串，如果可以在字符串任意位置添加字符，最少添加几个能让字符串整体都是回文串。
1
2
3
4
5
6
7
8
9
10
思路：
L做行，R做列的二维db表,dp[i][j]表示，str(i..j)位置上的字符串最少要多少个字符才是回文串
L > R的下半部分区域无效，对角线L == R，必然都是 0 个字符
第二条对角线 [0,1]..[1,2]，0位置字符等于1位置字符则 dp[0][1] = 0,若不等，则补一个字符dp[0][1] = 1...第二条对角线以此类推，要么0要么1

dp[i][j]
三种情况：
dp[i][j] = dp[i][j-1] + 1 //j位置不动，搞定i..j-1位置，再补1个
dp[i][j] = dp[i+1][j] + 1 //i位置不动，搞定i+1..j位置，再补1个
dp[i][j] = dp[i+1][j-1] //只有刚好i位置字符 = j位置的字符，才有这种情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public static String getPalindrome1(String str) {
    if (str == null || str.length() < 2) {
        return str;
    }
    char[] chas = str.toCharArray();
    int[][] dp = getDP(chas);
    char[] res = new char[chas.length + dp[0][chas.length - 1]];
    int i = 0;
    int j = chas.length - 1;
    int resl = 0;
    int resr = res.length - 1;
    while (i <= j) {
        if (chas[i] == chas[j]) {
            res[resl++] = chas[i++];
            res[resr--] = chas[j--];
        } else if (dp[i][j - 1] < dp[i + 1][j]) {
            res[resl++] = chas[j];
            res[resr--] = chas[j--];
        } else {
            res[resl++] = chas[i];
            res[resr--] = chas[i++];
        }
    }
    return String.valueOf(res);
}

public static int[][] getDP(char[] str) {
    int[][] dp = new int[str.length][str.length];
    for (int j = 1; j < str.length; j++) {
        dp[j - 1][j] = str[j - 1] == str[j] ? 0 : 1;
        for (int i = j - 2; i > -1; i--) {
            if (str[i] == str[j]) {
                dp[i][j] = dp[i + 1][j - 1];
            } else {
                dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
            }
        }
    }
    return dp;
}
1
2
3
一种消息接收并打印的结构设计
已知一个消息流会不断地吐出整数 1~N，但不一定按照顺序吐出。如果上次打印的数为 i， 那么当 i+1 出现时，请打印 i+1 及其之后接收过的并且连续的所有数，直到 1~N 全部接收 并打印完，请设计这种接收并打印的结构。
初始时默认i==0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public static class Node {
    public String info;
    public Node next;

    public Node(String str) {
        info = str;
    }
}

public static class MessageBox {
    //头尾链表
    private HashMap<Integer, Node> headMap;
    private HashMap<Integer, Node> tailMap;
    private int waitPoint;

    public MessageBox() {
        headMap = new HashMap<Integer, Node>();
        tailMap = new HashMap<Integer, Node>();
        waitPoint = 1;
    }

    // 消息的编号，info消息的内容, 消息一定从1开始
    public void receive(int num, String info) {
        if (num < 1) {
            return;
        }
        Node cur = new Node(info);
        // num~num
        headMap.put(num, cur);
        tailMap.put(num, cur);
        // 建立了num~num这个连续区间的头和尾
        // 查询有没有某个连续区间以num-1结尾
        if (tailMap.containsKey(num - 1)) {
            tailMap.get(num - 1).next = cur;
            tailMap.remove(num - 1);
            headMap.remove(num);
        }
        // 查询有没有某个连续区间以num+1开头的
        if (headMap.containsKey(num + 1)) {
            cur.next = headMap.get(num + 1);
            tailMap.remove(num);
            headMap.remove(num + 1);
        }
        if (num == waitPoint) {
            print();
        }
    }

    private void print() {
        Node node = headMap.get(waitPoint);
        headMap.remove(waitPoint);
        while (node != null) {
            System.out.print(node.info + " ");
            node = node.next;
            waitPoint++;
        }
        tailMap.remove(waitPoint-1);
        System.out.println();
    }
}
1
现有n1+n2种面值的硬币，其中前n1种为普通币，可以取任意枚，后n2种为纪念币， 每种最多只能取一枚，每种硬币有一个面值，问能用多少种方法拼出m的面值?
1
2
3
4
思路：
以普通币做行，面值做列，dp1[i][j]存储有多少种方法
以纪念币做行，面值做列，dp2[i][j]存储有多少种方法
最后结果：两个动态规划表的最后一行结果乘积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public static int moneyWays(int[] arbitrary, int[] onlyone, int money) {
    if (money < 0) {
        return 0;
    }
    if ((arbitrary == null || arbitrary.length == 0) && (onlyone == null || onlyone.length == 0)) {
        return money == 0 ? 1 : 0;
    }
    // 任意张 的数组， 一张的数组，不可能都没有
    int[][] dparb = getDpArb(arbitrary, money);
    int[][] dpone = getDpOne(onlyone, money);
    if (dparb == null) { // 任意张的数组没有，一张的数组有
        return dpone[dpone.length - 1][money];
    }
    if (dpone == null) { // 任意张的数组有，一张的数组没有
        return dparb[dparb.length - 1][money];
    }
    int res = 0;
    for (int i = 0; i <= money; i++) {
        res += dparb[dparb.length - 1][i] * dpone[dpone.length - 1][money - i];
    }
    return res;
}

public static int[][] getDpArb(int[] arr, int money) {
    if (arr == null || arr.length == 0) {
        return null;
    }
    int[][] dp = new int[arr.length][money + 1];
    // dp[i][j] 0..i券 自由选择张数， 搞定j元， 有多少方法？

    for (int i = 0; i < arr.length; i++) {
        dp[i][0] = 1;
    }
    // [0] 5元 0元 5元 10元 15元 20元
    for (int j = 1; arr[0] * j <= money; j++) {
        dp[0][arr[0] * j] = 1;
    }
    // 0行 0列 填完了
    for (int i = 1; i < arr.length; i++) {
        for (int j = 1; j <= money; j++) {
            dp[i][j] = dp[i - 1][j];
            dp[i][j] += j - arr[i] >= 0 ? dp[i][j - arr[i]] : 0;
        }
    }
    return dp;
}

public static int[][] getDpOne(int[] arr, int money) {
    if (arr == null || arr.length == 0) {
        return null;
    }
    int[][] dp = new int[arr.length][money + 1];
    for (int i = 0; i < arr.length; i++) {
        dp[i][0] = 1;
    }
    if (arr[0] <= money) {
        dp[0][arr[0]] = 1;
    }
    for (int i = 1; i < arr.length; i++) {
        for (int j = 1; j <= money; j++) {
            dp[i][j] = dp[i - 1][j];
            dp[i][j] += j - arr[i] >= 0 ? dp[i - 1][j - arr[i]] : 0;
        }
    }
    return dp;
}
1
2
3
给定一个正数N，表示你在纸上写下1~N所有的数字

返回在书写的过程中，一共写下了多少个1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
思路：
假设N的高位数是1的情况,假设N = 13625， 将函数拆成:
f(13625) = (3626..13625)非递归的1次数 + f(3625)
f(3625) = (626..3625)非递归的1次数 + f(625)...依次递归下去


求(3626..13625)非递归的1次数，13625的长度是k=5:
高位是1 ： N % 10^(k-1) + 1 （这是高位1固定的情况下，能得到的1）
个十百千： (k-1) * 10^(k-2) (K-1表示个十百千，四种变化，后面10^3，表示固定某个1之后，其他三个位置的变化可能性)
上面两种可能性相加，就是(3626..13625)范围上，1出现的次数

假设N的高位不是1的情况，假设N = 3625
千位是1：必定是1000~1999，所以是10^(k-1)
个十百：分段[626~1625]、[1626~2625]、[2626~3625]，个十百三个位置定一个是1，其他位置变化
       所以是 千位数的值 * (K-1) * 10^(K-2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public static int solution2(int num) {
    if (num < 1) {
        return 0;
    }
    // num -> 13625
    // len = 5位数
    int len = getLenOfNum(num);
    if (len == 1) {
        return 1;
    }
    // num 13625
    // tmp1 10000
    // num 7872328738273
    // tmp1 1000000000000
    int tmp1 = powerBaseOf10(len - 1);
    // num最高位 num / tmp1
    int first = num / tmp1;
    // 最高1 N % tmp1 + 1
    // 最高位first tmp1
    int firstOneNum = first == 1 ? num % tmp1 + 1 : tmp1;
    // 除去最高位之外，剩下1的数量
    // 最高位1 10(k-2次方) * (k-1) * 1
    // 最高位first 10(k-2次方) * (k-1) * first
    int otherOneNum = first * (len - 1) * (tmp1 / 10);
    return firstOneNum + otherOneNum + solution2(num % tmp1);
}

public static int getLenOfNum(int num) {
    int len = 0;
    while (num != 0) {
        len++;
        num /= 10;
    }
    return len;
}

public static int powerBaseOf10(int base) {
    return (int) Math.pow(10, base);
}
1
先给出可整合数组的定义:如果一个数组在排序之后，每相邻两个数差的绝对值 都为 1， 则该数组为可整合数组。例如，[5,3,4,6,2]排序之后为[2,3,4,5,6]， 符合每相邻两个数差的绝对值 都为 1，所以这个数组为可整合数组。 给定一个整型数组 arr，请返回其中最大可整合子数组的长度。例如， [5,5,3,2,6,4,3]的最大可整合子数组为[5,3,2,6,4]，所以返回 5。
1
2
3
4
思路：
转换可整合数组概念：
1.子数组中不能有重复值
2.子数组中的Max - Min = length - 1 ，则它是可整合数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static int getLIL2(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int len = 0;
    int max = 0;
    int min = 0;
    HashSet<Integer> set = new HashSet<Integer>();
    for (int L = 0; L < arr.length; L++) { // L 左边界
        set.clear();
        max = Integer.MIN_VALUE;
        min = Integer.MAX_VALUE;
        for (int R = L; R < arr.length; R++) { // R 右边界
            // arr[L..R]这个子数组在验证
            if (set.contains(arr[R])) {
                // arr[L..R]上开始 出现重复值了，arr[L..R往后]不需要验证了，
                // 一定不是可整合的
                break;
            }
            // arr[L..R]上无重复值
            set.add(arr[R]);
            max = Math.max(max, arr[R]);
            min = Math.min(min, arr[R]);
            if (max - min == R - L) { // L..R 是可整合的
                len = Math.max(len, R - L + 1);
            }
        }
    }
    return len;
}

卡特兰数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
k(0) = 1, k(1) = 1时，如果接下来的项满足：
k(n) = k(0) * k(n - 1) + k(1) * k(n - 2) + ... + k(n - 2) * k(1) + k(n - 1) * k(0)
或者
k(n) = c(2n, n) - c(2n, n-1) 数学排列组合公式
或者
k(n) = c(2n, n) / (n + 1)
就说这个表达式，满足卡特兰数，常用的是范式1和2，3几乎不会使用到

二叉树N个节点，能组成多少种结构（卡特兰数求法）？
其前几项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796...

最常见题目：
有N个0和N个1，要求组合排列后，任何位置的前缀的0的数量不比1的数量少
（等同于有三个值要入栈，求出栈的可能性，入栈的顺序肯定比出栈的顺序多，就会转换成卡特兰数问题）

股票问题

1
2
题目一：
给定一个数组arr，从左到右表示昨天从早到晚股票的价格。作为一个事后诸葛亮，你想知道如果只做一次交易，且每次交易只买卖一股，返回能挣到的最大钱数
1
2
3
4
5
6
7
8
9
10
11
12
public int maxProfit(int[] prices) {
    if (prices == null || prices.length == 0) {
        return 0;
    }
    int min = prices[0];
    int ans = 0;
    for (int i = 0; i < prices.length; i++) {
        min = Math.min(min, prices[i]);
        ans = Math.max(ans, prices[i] - min);
    }
    return ans;
}
1
2
3
4
题目二：
给定一个数组arr，从左到右表示昨天从早到晚股票的价格
作为一个事后诸葛亮，你想知道如果随便交易，
且每次交易只买卖一股，返回能挣到的最大钱数
1
2
3
思路：
假设位置是i,如果arr[i] > arr[i-1]，那么我获得arr[i] - arr[i-1]的利润
每个位置都这样做，等于求递增的差值
1
2
3
4
5
6
7
8
9
10
public static int maxProfit(int[] prices) {
    if (prices == null || prices.length == 0) {
        return 0;
    }
    int ans = 0;
    for (int i = 1; i < prices.length; i++) {
        ans += Math.max(prices[i] - prices[i-1], 0);
    }
    return ans;
}
1
2
3
4
题目三：
给定一个数组arr，从左到右表示昨天从早到晚股票的价格
作为一个事后诸葛亮，你想知 道如果交易次数不超过K次，
且每次交易只买卖一股，返回能挣到的最大钱数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
思路：
长度为N的数组arr，它的递增上坡数量一定是小于N/2的，因为要有上坡和下坡
最极限的例子：[1,5,3,4,2] 上下上下 也就是说最多的交易次数绝对不会大于N/2
若参数交易次数大于K次，等同于无限次交易，那么等同于题目二的解法

以index为行，K为列，建立dp表,dp[i][j]表示arr[0..i]上，交易次数小于等于j次的最大收益
dp[i][j]的可能性：
可能性一：
i位置不参与交易，dp[i][j] = dp[i-1][j]
可能性二：
i位置参与交易,并且i位置作为最后一次卖出股票的时机，等于求最后一次买入股票的时机
枚举[0..i][j-1]位置上的值 + arr[i] - arr[0..i]，求其中的最大值

可能性二的枚举行为加速：
dp[i-1][j] = MAX[0..i-1] -> (dp[0..i-1][j-1] - arr[0..i-1]) + arr[i-1]
假设缓存计算结果 t =  MAX[0..i-1] -> (dp[0..i-1][j-1] - arr[0..i-1])
dp[i][j] = MAX(t,dp[i][j-1] - arr[i]) + arr[i]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static int dp(int K, int[] prices) {
    if (prices == null || prices.length == 0) {
        return 0;
    }
    int N = prices.length;
    if (K >= N / 2) {
        return allTrans(prices);
    }
    int[][] dp = new int[N][K + 1];
    int ans = 0;
    for (int j = 1; j <= K; j++) {
        int t = dp[0][j - 1] - prices[0];
        for (int i = 1; i < N; i++) {
            t = Math.max(t, dp[i][j - 1] - prices[i]);
            dp[i][j] = Math.max(dp[i - 1][j], t + prices[i]);
            ans = Math.max(ans, dp[i][j]);
        }
    }
    return ans;
}

public static int allTrans(int[] prices) {
    int ans = 0;
    for (int i = 1; i < prices.length; i++) {
        ans += Math.max(prices[i] - prices[i - 1], 0);
    }
    return ans;
}

最后更新： 2021年02月03日 17:23

原始链接： https://midkuro.gitee.io/2020/10/31/algorithm-trainingcamp3/

赏
× 请我吃糖~
打赏二维码