密码学

密码学基本概念

密码在我们的生活中有着重要的作用，那么密码究竟来自何方，为何会产生呢？

密码学是网络安全、信息安全、区块链等产品的基础，常见的非对称加密、对称加密、散列函数等，都属于密码学范畴。

密码学有数千年的历史，从最开始的替换法到如今的非对称加密算法，经历了古典密码学，近代密码学和现代密码学三个阶段。密码学不仅仅是数学家们的智慧，更是如今网络空间安全的重要基础。

古典密码学

在古代的战争中，多见使用隐藏信息的方式保护重要的通信资料。比如先把需要保护的信息用化学药水写到纸上，药水干后，纸上看不出任何的信息，需要使用另外的化学药水涂抹后才可以阅读纸上的信息。

这些方法都是在保护重要的信息不被他人获取，但藏信息的方式比较容易被他人识破，例如增加哨兵的排查力度，就会发现其中的猫腻，因而随后发展出了较难破解的古典密码学。

替换法

替换法很好理解，就是用固定的信息将原文替换成无法直接阅读的密文信息。例如将 b 替换成 w ，e 替换成p ，这样bee 单词就变换成了wpp，不知道替换规则的人就无法阅读出原文的含义。

替换法有单表替换和多表替换两种形式。单表替换即只有一张原文密文对照表单，发送者和接收者用这张表单来加密解密。在上述例子中，表单即为：a b c d e - s w t r p 。

多表替换即有多张原文密文对照表单，不同字母可以用不同表单的内容替换。

例如约定好表单为：表单 1：abcde-swtrp 、表单2：abcde-chfhk 、表单 3：abcde-jftou。

规定第一个字母用第三张表单，第二个字母用第一张表单，第三个字母用第二张表单，这时 bee单词就变成了

(312)fpk ，破解难度更高，其中 312 又叫做密钥，密钥可以事先约定好，也可以在传输过程中标记出来。

移位法

移位法就是将原文中的所有字母都在字母表上向后（或向前）按照一个固定数目进行偏移后得出密文，典型的移位法应用有 “ 恺撒密码 ”。

例如约定好向后移动2位（abcde - cdefg），这样 bee 单词就变换成了dgg。

同理替换法，移位法也可以采用多表移位的方式，典型的多表案例是“维尼吉亚密码”（又译维热纳尔密码），属于多表密码的一种形式。

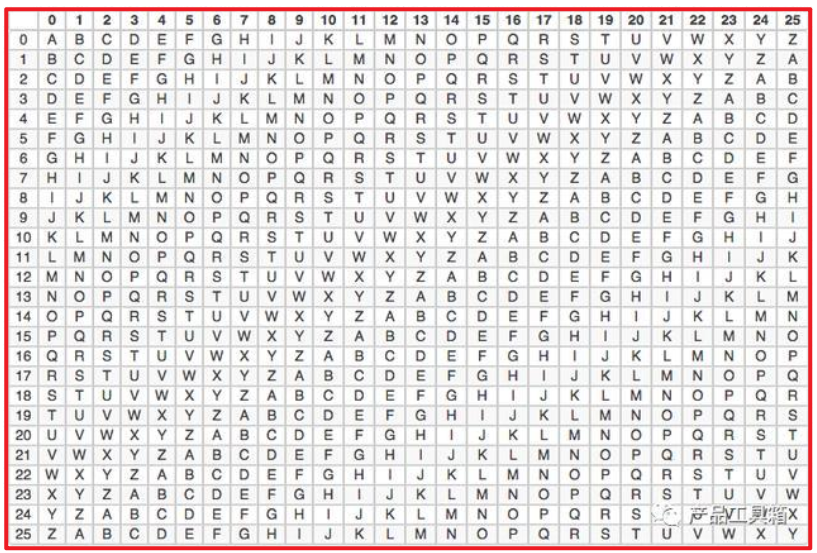
cryptography-1

古典密码破解方式

古典密码虽然很简单，但是在密码史上是使用的最久的加密方式，直到“概率论”的数学方法被发现，古典密码就被破解了。

cryptography-2

英文单词中字母出现的频率是不同的，e以12.702%的百分比占比最高，z 只占到0.074%，感兴趣的可以去百科查字母频率详细统计数据。如果密文数量足够大，仅仅采用频度分析法就可以破解单表的替换法或移位法。

cryptography-3

多表的替换法或移位法虽然难度高一些，但如果数据量足够大的话，也是可以破解的。以维尼吉亚密码算法为例，破解方法就是先找出密文中完全相同的字母串，猜测密钥长度，得到密钥长度后再把同组的密文放在一起，使用频率分析法破解。

近代密码学

古典密码的安全性受到了威胁，外加使用便利性较低，到了工业化时代，近现代密码被广泛应用。

恩尼格玛机是二战时期纳粹德国使用的加密机器，后被英国破译，参与破译的人员有被称为计算机科学之父、人工智能之父的图灵。

cryptography-4

恩尼格玛机使用的加密方式本质上还是移位和替代，只不过因为密码表种类极多，破解难度高，同时加密解密机器化，使用便捷，因而在二战时期得以使用。

现代密码学

散列函数

散列函数，也叫杂凑函数、摘要函数或哈希函数，可将任意长度的消息经过运算，变成固定长度数值，常见的有MD5、SHA-1、SHA256，多应用在文件校验，数字签名中。

MD5 可以将任意长度的原文生成一个128位（16字节）的哈希值

SHA-1可以将任意长度的原文生成一个160位（20字节）的哈希值

对称密码

对称密码应用了相同的加密密钥和解密密钥。对称密码分为：序列密码(流密码)，分组密码(块密码)两种。流密码是对信息流中的每一个元素（一个字母或一个比特）作为基本的处理单元进行加密，块密码是先对信息流分块，再对每一块分别加密。

例如原文为1234567890，流加密即先对1进行加密，再对2进行加密，再对3进行加密……最后拼接成密文；块加密先分成不同的块，如1234成块，5678成块，90XX(XX为补位数字)成块，再分别对不同块进行加密，最后拼接成密文。前文提到的古典密码学加密方法，都属于流加密。

非对称密码

对称密码的密钥安全极其重要，加密者和解密者需要提前协商密钥，并各自确保密钥的安全性，一但密钥泄露，即使算法是安全的也无法保障原文信息的私密性。

在实际的使用中，远程的提前协商密钥不容易实现，即使协商好，在远程传输过程中也容易被他人获取，因此非对称密钥此时就凸显出了优势。

非对称密码有两支密钥，公钥（publickey）和私钥（privatekey），加密和解密运算使用的密钥不同。用公钥对原文进行加密后，需要由私钥进行解密；用私钥对原文进行加密后（此时一般称为签名），需要由公钥进行解密（此时一般称为验签）。公钥可以公开的，大家使用公钥对信息进行加密，再发送给私钥的持有者，私钥持有者使用私钥对信息进行解密，获得信息原文。因为私钥只有单一人持有，因此不用担心被他人解密获取信息原文。

如何设置密码才安全

  • 密码不要太常见，不要使用类似于123456式的常用密码。
  • 各应用软件密码建议不同，避免出现一个应用数据库被脱库，全部应用密码崩塌，
  • 可在设置密码时增加注册时间、注册地点、应用特性等方法。例如tianjin123456，表示在天津注册的该应用。

ASCII编码

ASCII（American Standard Code for Information Interchange，美国信息交换标准代码）是基于拉丁字母的一套电脑编码系统，主要用于显示现代英语和其他西欧语言。它是现今最通用的单字节编码系统，并等同于国际标准ISO/IEC 646。

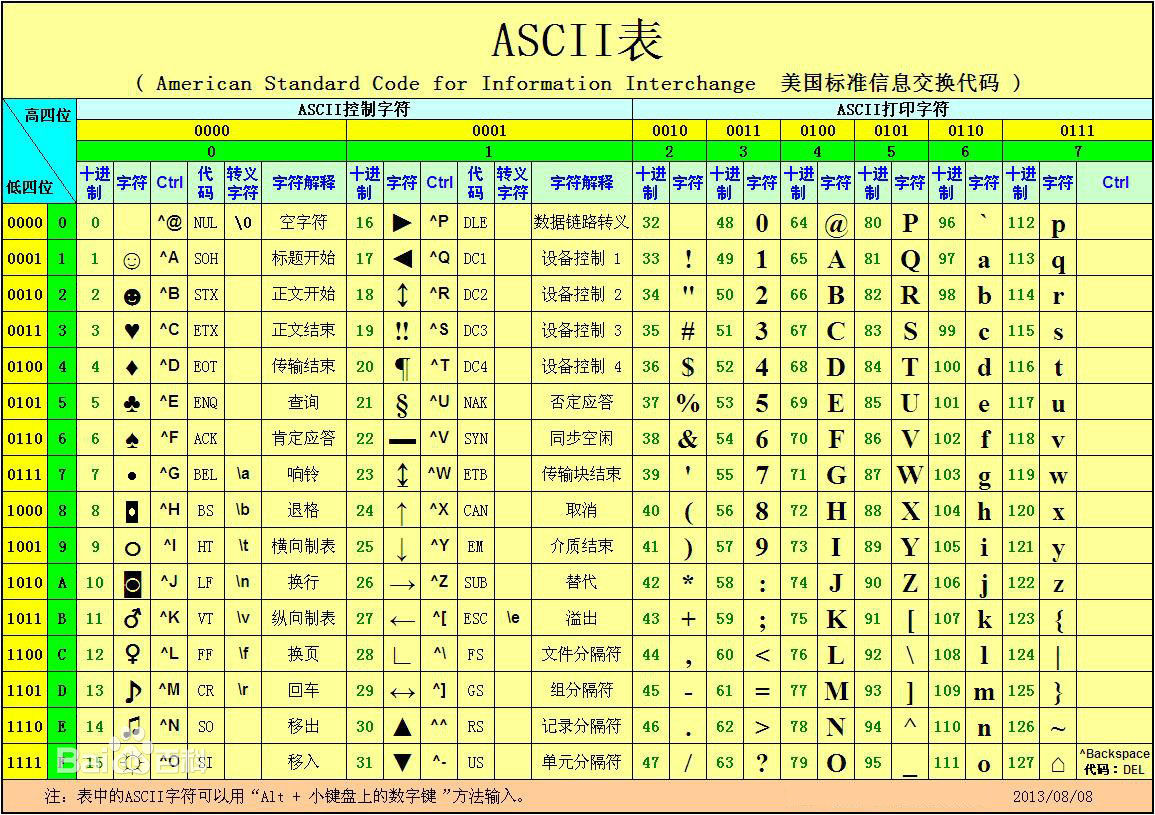
cryptography-5

创建Maven项目，添加pom.xml依赖

1
2
3
4
5
6
7
<dependencies>
    <dependency>
        <groupId>commons-io</groupId>
        <artifactId>commons-io</artifactId>
        <version>2.6</version>
    </dependency>
</dependencies>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class AsciiDemo {
    public static void main(String[] args) {
        char a = 'A';
        int b = a;
        // 打印ascii码
        System.out.println(b);  //65
        
        String a = "AaZ";
        // 获取ascii码，需要把字符串转成字符
        char[] chars = a.toCharArray();
        for (char c : chars) {
            int asciiCode = c;
            System.out.println(asciiCode); //65 97 90
        }
    }
}

恺撒加密

凯撒密码

在密码学中，恺撒密码是一种最简单且最广为人知的加密技术。

凯撒密码最早由古罗马军事统帅盖乌斯·尤利乌斯·凯撒在军队中用来传递加密信息，故称凯撒密码。这是一种位移加密方式，只对26个字母进行位移替换加密，规则简单，容易破解。下面是位移1次的对比：

cryptography-6

将明文字母表向后移动1位，A变成了B，B变成了C……，Z变成了A。同理，若将明文字母表向后移动3位：

cryptography-7

则A变成了D，B变成了E……，Z变成了C。

字母表最多可以移动25位。凯撒密码的明文字母表向后或向前移动都是可以的，通常表述为向后移动，如果要向前移动1位，则等同于向后移动25位，位移选择为25即可。

它是一种替换加密的技术，明文中的所有字母都在字母表上向后（或向前）按照一个固定数目进行偏移后被替换成密文。

例如，当偏移量是3的时候，所有的字母A将被替换成D，B变成E，以此类推。

这个加密方法是以恺撒的名字命名的，当年恺撒曾用此方法与其将军们进行联系。

恺撒密码通常被作为其他更复杂的加密方法中的一个步骤。

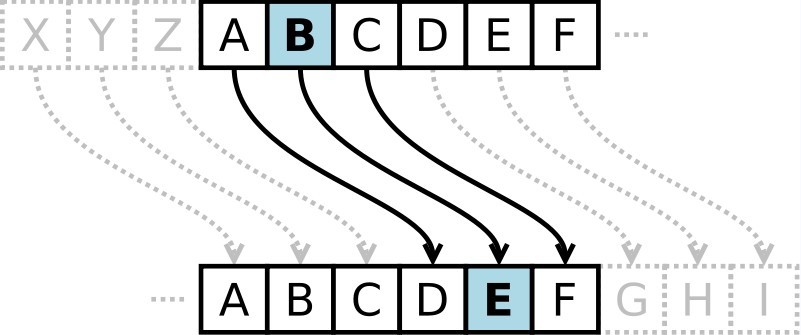
cryptography-8

简单来说就是当秘钥为n，其中一个待加密字符ch，加密之后的字符为ch+n，当ch+n超过’z’时，回到’a’计数。

凯撒位移加密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//把 hello world 往右边移动3位
public class KaiserDemo {
    public static void main(String[] args) {
        String input = "Hello world";
        // 往右边移动3位
        int key = 3;
        // 用来拼接
        StringBuilder sb = new StringBuilder();
        // 字符串转换成字节数组
        char[] chars = input.toCharArray();
        for (char c : chars) {
            int asciiCode = c;
            // 移动3位
            asciiCode = asciiCode + key;
            char newChar = (char) asciiCode;
            sb.append(newChar);
        }
    
        System.out.println(sb.toString()); //khoor#zruog
    }
}

凯撒加密和解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class KaiserDemo {
    public static void main(String[] args) {
        String orignal = "Hello world";
        // 往右边偏移三位
        int key = 3;
        // 选中我即将抽取的代码，按快捷键Ctrl + Alt + M 
        String encryptKaiser =  encryptKaiser(orignal,key);
        System.out.println("加密：" + encryptKaiser);
        String decryptKaiser =  decryptKaiser(encryptKaiser,key);
        System.out.println("解密：" + decryptKaiser);
    }
    /**
     * 使用凯撒加密方式解密数据
     *
     * @param encryptedData :密文
     * @param key           :密钥
     * @return : 源数据
     */
    public static String decryptKaiser(String encryptedData, int key) {
        // 将字符串转为字符数组
        char[] chars = encryptedData.toCharArray();
        StringBuilder sb = new StringBuilder();
        for (char aChar : chars) {
            // 获取字符的ASCII编码
            int asciiCode = aChar;
            // 偏移数据
            asciiCode -= key;
            // 将偏移后的数据转为字符
            char result = (char) asciiCode;
            // 拼接数据
            sb.append(result);
        }
        return sb.toString();
    }
    /**
     * 使用凯撒加密方式加密数据
     *
     * @param orignal :原文
     * @param key     :密钥
     * @return :加密后的数据
     */
    public static String encryptKaiser(String orignal, int key) {
        // 将字符串转为字符数组
        char[] chars = orignal.toCharArray();
        StringBuilder sb = new StringBuilder();
        for (char aChar : chars) {
            // 获取字符的ascii编码
            int asciiCode = aChar;
            // 偏移数据
            asciiCode += key;
            // 将偏移后的数据转为字符
            char result = (char) asciiCode;
            // 拼接数据
            sb.append(result);
        }
        return sb.toString();
    }
}

频度分析法

加密者选择将组成信息的字母替代成别的字母，比如说将a写成1，这样就不能被解密者直接拿到信息了。

这难不倒解密者，以英文字母为例，为了确定每个英文字母的出现频率，分析一篇或者数篇普通的英文文章，英文字母出现频率最高的是e，接下来是t，然后是a……，然后检查要破解的密文，也将每个字母出现的频率整理出来，假设密文中出现频率最高的字母是j，那么就可能是e的替身，如果密码文中出现频率次高的但是P，那么可能是t的替身，以此类推便就能解开加密信息的内容。这就是频率分析法。

  • 将明文字母的出现频率与密文字母的频率相比较的过程
  • 通过分析每个符号出现的频率而轻易地破译代换式密码
  • 在每种语言中，冗长的文章中的字母表现出一种可对之进行分辨的频率。
  • e是英语中最常用的字母，其出现频率为八分之一

运行计算article.txt文本中各个符号的出现次数，如下：

cryptography-9

然后对该文本进行位移3位，得到密文报，并在此统计密文的符号出现次数：

cryptography-10

运行结果 # 出现次数最多， 我们知道在英文当中 e 出现的频率是最高的，我们假设现在 # 号，就是 e ，变形而来的 ，我们可以对照 ascii 编码表 ，我们的凯撒加密当中位移是加了一个 key ，所以我们 猜测 两个值直接相差 -66 ，我们现在就以 -66 进行解密 生成一个文件，我们查看第一个文件发现，根本读不懂，所以解密失败，我们在猜测 h 是 e ，h 和 e 之间相差3 ，所以我们在去看第二个解密文件，发现我们可以读懂，解密成功。

cryptography-11

最后更新： 2020年11月13日 13:52

原始链接： https://midkuro.gitee.io/2020/05/29/cryptography-base/

赏
× 请我吃糖~
打赏二维码